
已知函数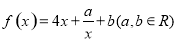 为奇函数.
为奇函数.
(1)若 ,求函数
,求函数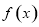 的解析式;
的解析式;
(2)当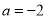 时,不等式
时,不等式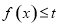 在
在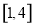 上恒成立,求实数
上恒成立,求实数 的最小值;
的最小值;
(3)当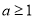 时,求证:函数
时,求证:函数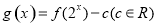 在
在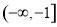 上至多一个零点.
上至多一个零点.
(1) ;(2)
;(2)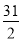 ;(3)证明略
;(3)证明略
【解析】
试题分析:(1)已知函数的奇偶性求参数的值一般思路:利用函数的奇偶性的定义转化为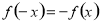 ,从而建立方程,使问题获解,但是在解决选择题,填空题时,利用定义去做相对麻烦,因此为使问题解决更快,可采用特值法;(2)对于恒成立的问题,常用到两个结论:(1)
,从而建立方程,使问题获解,但是在解决选择题,填空题时,利用定义去做相对麻烦,因此为使问题解决更快,可采用特值法;(2)对于恒成立的问题,常用到两个结论:(1)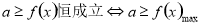 ,(2)
,(2)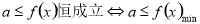 ;(3)对于给出的具体函数的解析式的函数,证明或判断在某区间上的单调性有两种方法:一是利用函数单调性的定义:作差、变形,由
;(3)对于给出的具体函数的解析式的函数,证明或判断在某区间上的单调性有两种方法:一是利用函数单调性的定义:作差、变形,由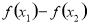 的符号,在确定符号是变形是关键,掌握配方,提公因式的方法,确定结论;二是利用函数的导数求解;(4)单调函数最多只有一个零点.
的符号,在确定符号是变形是关键,掌握配方,提公因式的方法,确定结论;二是利用函数的导数求解;(4)单调函数最多只有一个零点.
试题解析:【解析】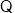 函数
函数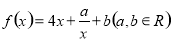 为奇函数,
为奇函数,
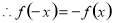 ,即
,即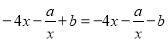

又 ,
,
 函数解析式
函数解析式
当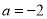 时,
时,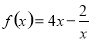
 函数
函数 在
在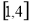 都是单调递增,
都是单调递增,
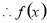 在
在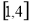 单调递增,
单调递增,
所以当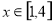 时,
时,
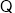 不等式
不等式 在
在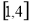 上恒成立,
上恒成立,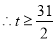
 实数
实数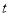 的最小值为
的最小值为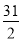
证明: ,设任取任意实数
,设任取任意实数




 ,
, ,即
,即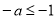
 ,又
,又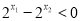 ,
,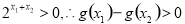 ,即
,即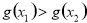
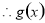 在
在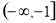 单调递减
单调递减
又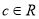 ,结合函数图象知函数
,结合函数图象知函数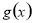 在
在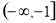 上至多有一个零点
上至多有一个零点
考点:1、利用函数的奇偶性求参数;2、恒成立的问题;3、利用定义证明函数的单调性


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com