
| y | x |
| y |
| x |
| y |
| x |
| 32+22 |
| 13 |
| 32+22 |
| 13 |
| 13 |
| 13 |
| y |
| x |
| |3k-2| | ||
|
3-
| ||
| 4 |
3+
| ||
| 4 |
| y |
| x |
3-
| ||
| 4 |
3+
| ||
| 4 |
| |3+2-t| | ||
|
| 2 |
| 2 |
| 2 |
| 2 |


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
| t |
| x |
| x2 |
| 2 |
| m2+1 |
| m |
查看答案和解析>>
科目:高中数学 来源:2008年普通高等学校招生全国统一考试上海卷数学理科 题型:013
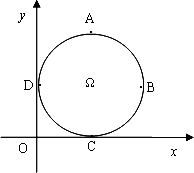
如图,在平面直角坐标系中,Ω是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、![]() 满足x≤
满足x≤![]() 且y≥
且y≥![]() ,则称P优于
,则称P优于![]() ,如果Ω中的点Q满足:不存在Ω中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧
,如果Ω中的点Q满足:不存在Ω中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com