
����Ŀ��ij������ֲ��ԡ�һ�߶���Ԯ���͡���ѵ��Ͷ��ֱ�滮���£�2018�꣬�þ��ֲ��ڡ�һ�߶���Ԯ��Ͷ���ʽ�Ϊ16000��Ԫ������ѵ��Ͷ���ʽ�Ϊ1000��Ԫ.�ƻ�ÿ�ꡰһ�߶���Ԯ��Ͷ�����һ�����һ�룬����ѵ��Ͷ�����һ������һ��.
��1��������һ��þ��ֲ���һ�߶���Ԯ���͡���ѵ��Ͷ���ܺ�����?
��2����2018����������2018�����þ��ֲ�����һ�꿪ʼ��һ�߶���Ԯ���͡���ѵ����Ͷ��֮�Ͳ�����62000��Ԫ?����Ͷ����ָ����Ͷ��֮�ͣ�
���𰸡���1��2020�꣬Ͷ���ܺ����٣���2��2022�꿪ʼ����Ͷ��֮�Ͳ�����62000��.
��������
��1����2018���������n�ꡰһ�߶���Ԯ��Ͷ���ʽ�Ϊan������ѵ��Ͷ���ʽ�Ϊbn��Ͷ���ܺ�Ϊcn��д������{cn}��ͨ�ʽ�����û�������ʽ���ɵó����ۣ�
��2�����ݵȱ����е����ʽ�ó�ǰn�����Ͷ��֮�ͣ��в���ʽ���n���ɣ�
��1����2018���������n�ꡰһ�߶���Ԯ��Ͷ���ʽ�Ϊan��
����ѵ��Ͷ���ʽ�Ϊbn��Ͷ���ܺ�Ϊcn��
��{an}����16000Ϊ�����![]() Ϊ���ȵĵȱ����У�
Ϊ���ȵĵȱ����У�
{bn}����1000Ϊ�����2Ϊ���ȵĵȱ����У�
![]() ��
��![]() ��
��
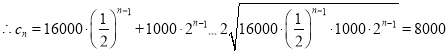 ��
��
���ҽ���![]() ����
����![]() ʱȡ�Ⱥţ�
ʱȡ�Ⱥţ�
����2020�꣬�þ��ֲ���һ�߶���Ԯ���͡���ѵ��Ͷ���ܺ����٣�
��2����{cn}��ǰ���ΪTn��
��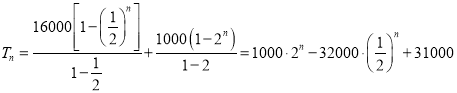 ��
��
��![]() ��
��
��![]() ����
����![]() �����
�����![]() ��
��![]() ����ȥ����
����ȥ����
��![]() ��
��![]() ��
��
���Դ�2018������ĵ�5�꼴2022�꿪ʼ����һ�߶���Ԯ���͡���ѵ����Ͷ��֮�Ͳ�����62000��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���������IJ�Ʒ![]() ��ֱ����λ������
��ֱ����λ������![]() �ڣ���λ��
�ڣ���λ�� ![]() ).������һ����Ʒ
).������һ����Ʒ![]() ��ֱ��λ������
��ֱ��λ������![]() �ڸó��ɻ����ֱ�Ϊ10��30��20��10(��λ��Ԫ�����ִӸó������IJ�Ʒ
�ڸó��ɻ����ֱ�Ϊ10��30��20��10(��λ��Ԫ�����ִӸó������IJ�Ʒ![]() �������ȡ200���������ǵ�ֱ�����õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
�������ȡ200���������ǵ�ֱ�����õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
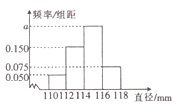
��1����![]() ��ֵ�������Ƹó�����һ��
��ֵ�������Ƹó�����һ��![]() ��Ʒ��ƽ������
��Ʒ��ƽ������
��2�����÷ֲ��������ֱ��λ������![]() �ڵIJ�Ʒ�������ȡһ������Ϊ5���������������������ȡ������Ʒ���м�⣬��������Ʒ��������һ����Ʒ��ֱ��λ������
�ڵIJ�Ʒ�������ȡһ������Ϊ5���������������������ȡ������Ʒ���м�⣬��������Ʒ��������һ����Ʒ��ֱ��λ������![]() �ڵĘ���.
�ڵĘ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() ������
������![]() .
.
��1����![]() ʱ������
ʱ������![]() ��ֵ��
��ֵ��
��2����������![]() ������
������![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ʱ����
ʱ����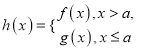 ����
����![]() ����СֵΪ
����СֵΪ![]() ����ʵ��
����ʵ��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P��ֱ��y����4�ľ���ȵ�P����A��0��1���ľ����3��
��1�����P�Ĺ켣���̣�
��2��������Q��0��2���Ķ�ֱ��l���P�Ĺ콻��M��N���㣬�Ƿ���ڶ���Rʹ�á�MRQ����NRQ�������ڣ������R�����꣺�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʵ��![]() ��������ʵ��
��������ʵ��![]() ��ʹ����ʽ
��ʹ����ʽ![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��ΧΪ________.
��ȡֵ��ΧΪ________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Բ![]() ����Բ��������ԭ��O���뾶Ϊ
����Բ��������ԭ��O���뾶Ϊ![]() ��Բ����ԲC��������Բ������֪��ԲC����������ֱ���
��Բ����ԲC��������Բ������֪��ԲC����������ֱ���![]() .
.
��1������ԲC��һ����![]() ����
����![]() ������ԲC����������Բ���ķ��̣�
������ԲC����������Բ���ķ��̣�
��2���ڣ�1���������£�����![]() ��ֱ��l����ԲCֻ��һ�����㣬�ҽ���ԲC��������Բ�������ҳ�Ϊ
��ֱ��l����ԲCֻ��һ�����㣬�ҽ���ԲC��������Բ�������ҳ�Ϊ![]() ����P������ꣻ
����P������ꣻ
��3����֪![]() ���Ƿ����a��b��ʹ��ԲC��������Բ���ϵĵ㵽������
���Ƿ����a��b��ʹ��ԲC��������Բ���ϵĵ㵽������![]() ��ֱ�ߵ���̾���
��ֱ�ߵ���̾���![]() .�����ڣ����a��b��ֵ���������ڣ���˵������.
.�����ڣ����a��b��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
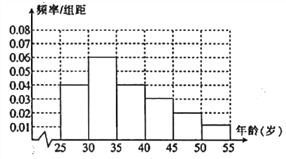
����Ŀ��ij��У�������ʵ������![]() �����Ⱥ�����ȡ 1000 �˽�����һ���Ƿ�ͨ�������ĵ��飬��ͨ��������Ϊ��ʱ���塱�������Ϊ����ʱ���塱.ͨ������õ����������������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��������
�����Ⱥ�����ȡ 1000 �˽�����һ���Ƿ�ͨ�������ĵ��飬��ͨ��������Ϊ��ʱ���塱�������Ϊ����ʱ���塱.ͨ������õ����������������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��������![]() �꣬
�꣬ ![]() ������������У���ʱ���塱�����ֱ�ռ����������
������������У���ʱ���塱�����ֱ�ռ����������![]() ��
��![]() .
.
��1����![]() ����
����![]() ������Ρ�ʱ���塱��������
������Ρ�ʱ���塱��������
��2����![]() ���
���![]() ������εġ�ʱ���塱�У����÷ֲ��������ȡ6�˲μ�����ʱ�д��˴���������������Ϊ��ӣ�����ӵ��������䶼��
������εġ�ʱ���塱�У����÷ֲ��������ȡ6�˲μ�����ʱ�д��˴���������������Ϊ��ӣ�����ӵ��������䶼��![]() ���ڵĸ��ʡ�
���ڵĸ��ʡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���ᄊ�����У�35���˶�Ա�ijɼ�����λ�����ӣ��ľ�Ҷͼ��ͼ��ʾ��

�����˶�Ա���ɼ��ɺõ����Ϊ1��35�ţ�����ϵͳ�����������г�ȡ5�ˣ������гɼ�������![]() �ϵ��˶�Ա����Ϊ
�ϵ��˶�Ա����Ϊ
A.6B.5C.4D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���õ���ʵũ���ʱ�֤���ƶȣ��Ϸ�ij���Ͷ����ϲ��ŵ�����![]() ���°������
���°������![]() ��ũ�����м��������Ǽ�������
��ũ�����м��������Ǽ�������![]() �������¹��ʣ��õ���
�������¹��ʣ��õ���![]() ��ũ���¹��ʵ���λ��Ϊ
��ũ���¹��ʵ���λ��Ϊ![]() ��Ԫ��������
��Ԫ��������![]() ��ũ���¹��ʾ���
��ũ���¹��ʾ���![]() ����Ԫ���ڣ����¹���������
����Ԫ���ڣ����¹���������![]() ����Ԫ���ڵ�����Ϊ
����Ԫ���ڵ�����Ϊ![]() �������ݵ�����������ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
�������ݵ�����������ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��

������![]() ��
��![]() ��ֵ��
��ֵ��
������֪��![]() ��ũ�����¹��ʸ���ƽ�����ļ�������
��ũ�����¹��ʸ���ƽ�����ļ�������![]() �����Ǽ�������
�����Ǽ�������![]() �������ܷ��ڷ�����ĸ��ʲ�����
�������ܷ��ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ�Dz��Ǽ��������¹����Ƿ����ƽ�����й�ϵ��
��ǰ������Ϊ�Dz��Ǽ��������¹����Ƿ����ƽ�����й�ϵ��
�ο���ʽ�����ݣ� ������
������![]() ��
��
|
|
|
|
|
|
|
|
|
|
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com