
分析 (1)解不等式|2x+a|<b便可得到$\frac{-b-a}{2}<x<\frac{b-a}{2}$,从而得到$\left\{\begin{array}{l}{\frac{-b-a}{2}=1}\\{\frac{b-a}{2}=2}\end{array}\right.$,这样即可解出a=-3,b=1;
(2)先得到$f(x)=\left\{\begin{array}{l}{-3x-7}&{x≤-3}\\{x+5}&{-3<x<-1}\\{3x+7}&{x≥-1}\end{array}\right.$,看出f(x)为分段函数,在每一段上可根据一次函数的单调性求出f(x)在每一段上的值域,最后便可得出f(x)的最小值.
解答 解:(1)由|2x+a|<b得-b<2x+a<b,即$\frac{-b-a}{2}<x<\frac{b-a}{2}$;
由题意,$\left\{\begin{array}{l}{\frac{-b-a}{2}=1}\\{\frac{b-a}{2}=2}\end{array}\right.$;
解得a=-3,b=1;
(2)f(x)=2|x+3|+|x+1|=$\left\{\begin{array}{l}{-3x-7}&{x≤-3}\\{x+5}&{-3<x<-1}\\{3x+7}&{x≥-1}\end{array}\right.$;
∴①x≤-3时,f(x)单调递减;
∴f(x)≥f(-3)=2;
②-3<x<-1时,f(x)单调递增;
∴f(-3)<f(x)<f(-1);
即2<f(x)<4;
③x≥-1时,f(x)单调递增;
∴f(x)≥f(-1)=4;
∴综上得f(x)的最小值为2.
点评 考查绝对值不等式的解法,含绝对值函数的处理方法:去绝对值号,分段函数最值的求法,以及根据一次函数的单调性求函数值域,从而得出函数最值的方法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 若a∥α,b∥α,则a∥b | B. | 若α⊥β,a?α,b?β,则a⊥b | ||
| C. | 若a⊥b,b⊥α,则a∥α | D. | 若α∥β,a?α,则a∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
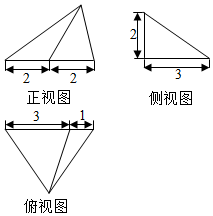
| A. | 4cm | B. | $\sqrt{13}$cm | C. | $\sqrt{14}$cm | D. | $\sqrt{15}$cm |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
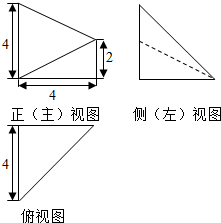
| A. | 4 | B. | 4$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com