分析:(1)取AB中点G,连结A1G、FG,由正方体的性质和平行四边形的判定证出四边形GFD1A1是平行四边形,从而 A1G∥D1F.设A1G、AE交于点H,在正方形ABA1B1中利用Rt△A1AG≌Rt△ABE,证出∠GA1A+∠A1AE=90°,得∠AHA1=90°即AE⊥A1G,从而证出AE⊥D1F;
(2)由正方体的性质和线面垂直的定义证出A1D1⊥AE,结合AE⊥D1F且A1D1、D1F1是平面A1D1F内的相交直线,可得AE⊥平面A1D1F.
解答:解:(1)取AB中点G,连结A
1G、FG
∵FG是正方形ABCD的对边中点的连线,∴FG
AD
∵A
1D
1AD,∴FG
A
1D
1,可得四边形GFD
1A
1是平行四边形,
所以A
1G∥D
1F.
设A
1G与AE相交于点H,∠AHA
1是AE与D
1F所成的角.
∵正方形ABA
1B
1中,G、E分别是AB、BB
1的中点,
∴Rt△A
1AG≌Rt△ABE,得∠GA
1A=∠BAE=90°-∠A
1AE
∴∠GA
1A+∠A
1AE=90°,得∠AHA
1=90°即AE⊥A
1G,
结合A
1G∥D
1F,得AE⊥D
1F;
(2)∵正方体ABCD-A
1B
1C
1D
1中,
A
1D
1⊥平面ABB
1A
1,且AE?平面ABB
1A
1,
∴A
1D
1⊥AE,
又∵AE⊥D
1F,A
1D
1∩D
1F
1=D
1,
∴AE⊥平面A
1D
1F.
点评:本题给出正方体的棱的中点,求证线线垂直和线面垂直.着重考查了正方体的性质、线面垂直的判定与性质、平行四边形的判定和全等三角形等知识,属于中档题.

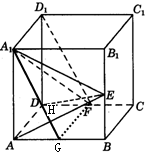
 如图,在正方体ABCD-A1B1C1D1,E、F分别是BB1、CD的中点.
如图,在正方体ABCD-A1B1C1D1,E、F分别是BB1、CD的中点.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则