
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据全称命题的否定是特称命题进行判断,
②根据相关性系数的性质进行判断,
③根据几何概型的概率公式进行判断,
④根据不等式恒成立进行判断.
解答 解:①命题“任意x∈R,x2≥0”的否定是“存在x0∈R,x02<0”,故①错误;
②根据线性相关系数r的意义可知,当r的绝对值越接近于1时,两个随机变量线性相关性越强,故②正确,
③若a,b∈[0,1],则不等式a2+b2<$\frac{1}{4}$成立的概率P=$\frac{\frac{1}{4}×π×(\frac{1}{2})^{2}}{1×1}$=$\frac{π}{16}$;故③错误,
④函数y=log2(x2-ax+2)在[2,+∞)上恒为正,
则log2(x2-ax+2)>0,即x2-ax+2>1,x2-ax+1>0恒成立,
即a<x+$\frac{1}{x}$在[2,+∞)上恒成立,
∵当x≥2时,y=x+$\frac{1}{x}$在[2,+∞)上为增函数,
∴当x=2时,x+$\frac{1}{x}$取得最小值2+$\frac{1}{2}$=$\frac{5}{2}$,
∴a<$\frac{5}{2}$.
则实数a的取值范围是(-∞,$\frac{5}{2}$).故④正确,
故正确的是:②④.
故选:B.
点评 本题主要考查命题的真假判断,涉及知识点较多,综合性较强,难度不大.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 模型1的相关指数R2为0.87 | B. | 模型2的相关指数R2为0.97 | ||
| C. | 模型3的相关指数R2为0.50 | D. | 模型4的相关指数R2为0.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}{\vec e_1}-\frac{1}{3}{\vec e_2}$ | B. | $\frac{2}{3}{\vec e_1}+\frac{4}{3}{\vec e_2}$ | C. | $\frac{1}{3}{\vec e_1}+\frac{2}{3}{\vec e_2}$ | D. | $\frac{2}{3}{\vec e_1}+\frac{1}{3}{\vec e_2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
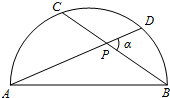
| A. | cosα | B. | sinα | C. | tanα | D. | $\frac{1}{tanα}$=cotα |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com