
已知函数
(1)求函数 的单调区间.
的单调区间.
(2)若方程 有4个不同的实根,求
有4个不同的实根,求 的范围?
的范围?
(3)是否存在正数 ,使得关于
,使得关于 的方程
的方程 有两个不相等的实根?如果存在,求b
有两个不相等的实根?如果存在,求b 满足的条件,如果不存在,说明理由.
满足的条件,如果不存在,说明理由.
(1)增区间为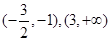 ,减区间为
,减区间为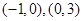 ;(2)
;(2) ;(3)不存在,理由见详解.
;(3)不存在,理由见详解.
解析试题分析:(1)首先求导函数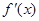 ,然后通过判断
,然后通过判断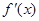 的符号可求得单调区间;(2)构造函数
的符号可求得单调区间;(2)构造函数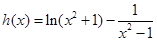 ,然后利用导数研究函数的取值变化,确定图象的位置,由图象可直观得到函
,然后利用导数研究函数的取值变化,确定图象的位置,由图象可直观得到函 的取值范围;(3)
的取值范围;(3)
试题解析:(1)根据 定义域后,求导得到
定义域后,求导得到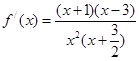 ,
,
根据导数和0的关系得到在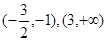 是函数
是函数 的增区间;在
的增区间;在 是函数
是函数 减区间.
减区间.
(2)(2)令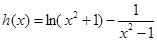 ,求导得
,求导得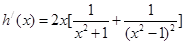 ,
,
里面有一个零点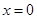 和两个断点
和两个断点 ,所以初步可以得到函数在区间
,所以初步可以得到函数在区间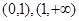 单调增;在区间
单调增;在区间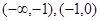 单调减.
单调减.
当 从负半轴方向趋近于-1时,
从负半轴方向趋近于-1时,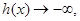
当 从正半轴方向趋近于-1时,
从正半轴方向趋近于-1时,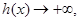
而且 时,
时,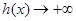 ,
,
而且可以很容易得到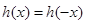 ,函数为偶函数,而且
,函数为偶函数,而且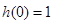 ,
,
另半边的图像就容易模拟得到了,所以 有4个不同的实根,结合图像得到
有4个不同的实根,结合图像得到 .
.
(本题必须另半边如果不分析必须用奇偶性说明;而且必须说明在断点处的趋势,否则扣2到3分)
(3)结论:这样的正数 不存在.
不存在.
假设存在满足条件的 ,使得方程
,使得方程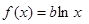 存在两个不相等的实根
存在两个不相等的实根 和
和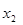 ,然后代入方程,根据其结构利用第(1)问的结论判断出
,然后代入方程,根据其结构利用第(1)问的结论判断出 在
在 上的取值及单调性,然后结合假设导出矛盾,作出判断.
上的取值及单调性,然后结合假设导出矛盾,作出判断.
假设存在正数 ,使得方程
,使得方程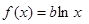 存在两个不相等的实根
存在两个不相等的实根 和
和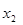 ,则
,则
根据定义域知道 和
和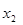 都是正数.
都是正数.
根据第1问知道,当 时,函数的最小值
时,函数的最小值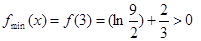 ,
,
所以 ,
,
因为 ,等式两边同号,所以,
,等式两边同号,所以,
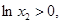 所以
所以

不妨设
由(1)(2)可得 ,
,
所以 ,
,
所以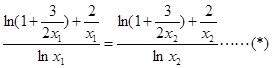 .
.
因为很容易证明到函数 在
在 为恒大于0且为减函数
为恒大于0且为减函数
所以(*)方程显然不成立,因为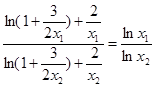 左边大于1,右边小于1.
左边大于1,右边小于1.
所以原假设:存在正数 ,使得方程
,使得方程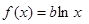 存在两个不相等的实根
存在两个不相等的实根 和
和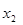 错误(本题其他证法,请酌情给分)
错误(本题其他证法,请酌情给分)
考点:1、导数与函数的单调性关系;2、探索性问题;3、函数与方程根的关系.


科目:高中数学 来源: 题型:解答题
某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3000平方米,其中场地四周(阴影部分)为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.
(1)分别写出用x表示y和S的函数关系式(写出函数定义域);
(2)怎样设计能使S取得最大值,最大值为多少?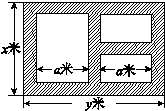
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
二次函数f(x)满足f(x+1)-f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)在区间[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,求实数m的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某通讯公司需要在三角形地带 区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域
区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域 内,乙中转站建在区域
内,乙中转站建在区域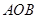 内.分界线
内.分界线 固定,且
固定,且 =
= 百米,边界线
百米,边界线 始终过点
始终过点 ,边界线
,边界线 满足
满足 .
.
设 (
( )百米,
)百米,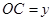 百米.
百米.
(1)试将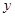 表示成
表示成 的函数,并求出函数
的函数,并求出函数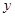 的解析式;
的解析式;
(2)当 取何值时?整个中转站的占地面积
取何值时?整个中转站的占地面积 最小,并求出其面积的最小值.
最小,并求出其面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
定义在 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数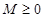 ,都有
,都有 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的一个上界.已知函数
的一个上界.已知函数 ,
, .
.
(1)若函数 为奇函数,求实数
为奇函数,求实数 的值;
的值;
(2)在(1)的条件下,求函数 在区间
在区间 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数 在
在 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知定义在R上的奇函数f(x)满足f(x-4)=-f(x).
(1)求f(2 012)的值;
(2)求证:函数f(x)的图像关于直线x=2对称;
(3)若f(x)在区间[0,2]上是增函数,试比较f(-25),f(11),f(80)的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com