
分析 (1)令n=10,可得a10.
(2)假设$\frac{98}{101}$是该数列的项,则$\frac{98}{101}$=$\frac{3n-2}{3n+1}$,解得n是否是正整数,即可判断出是否是该数列的项.
(3)an=$\frac{3n+1-3}{3n+1}$=1-$\frac{3}{3n+1}$.利用数列$\{\frac{3}{3n+1}\}$单调递减,可得数列$\{1-\frac{3}{3n+1}\}$单调递增,即可得出.
解答 解:(1)a10=$\frac{3×10-2}{3×10+1}$=$\frac{28}{31}$.
(2)假设$\frac{98}{101}$是该数列的项,则$\frac{98}{101}$=$\frac{3n-2}{3n+1}$,解得n=$\frac{100}{3}$∉N,因此$\frac{98}{101}$不是该数列的项.
(3)an=$\frac{3n-2}{3n+1}$=$\frac{3n+1-3}{3n+1}$=1-$\frac{3}{3n+1}$.
∵数列$\{\frac{3}{3n+1}\}$单调递减,
∴数列$\{1-\frac{3}{3n+1}\}$单调递增;
∴数列的最小项为a1=$\frac{1}{4}$,无最大项.
点评 本题考查了数列的通项公式、数列的单调性,考查了推理能力与计算能力,属于基础题.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(2,+∞) | B. | (-∞,0)∪(0,+∞) | C. | (0,2) | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年云南大理州南涧县民族中学高二文9月月考数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系 中,点
中,点 ,直线
,直线 ,设圆
,设圆 的半径为
的半径为 ,圆心在
,圆心在 上.
上.

(Ⅰ)若圆心 也在直线
也在直线 上,过点
上,过点 作圆
作圆 的切线,求切线的方程;
的切线,求切线的方程;
(Ⅱ)若圆 上存在点
上存在点 ,使
,使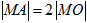 ,求圆心
,求圆心 的横坐标
的横坐标 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com