
【题目】已知圆![]() ,圆
,圆![]() ,圆
,圆![]() 与圆
与圆![]() 的公切线的条数的可能取值共有( )
的公切线的条数的可能取值共有( )
A. 2种B. 3种C. 4种D. 5种
【答案】D
【解析】
求出两圆的圆心距以及两圆半径之和和半径之差,结合两圆位置关系和切线条数关系进行判断即可.
两圆的圆心和半径分别为A(0,0),半径R=1, B(2,0),半径为r,
|AB|=2,半径之和为1+r,半径之差为r-1,
若两圆相外切,即1+r=2,即r=1时,此时两圆公切线有3条,
若两圆外离,则1+r<2,即0<r<1时,两圆公切线有4条,
若两圆相交,则r-1<2且2<1+r,即1<r<3时,两圆相交,此时公切线有2条,
若两圆内切,即r-1=2,即r=3时,此时两圆公切线有1条,
若两圆内含,即r-1>2,即r>3,此时两圆公切线为0条,
即圆A与圆B的公切线的条数的可能取值有5种,
故选:D.


科目:高中数学 来源: 题型:
【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目,若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
选考方案待确定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 选考方案确定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
选考方案待确定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
(Ⅰ)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(Ⅱ)假设男生、女生选择选考科目是相互独立的.从选考方案确定的8位男生随机选出1人,从选考方案确定的10位女生中随机选出1人,试求该男生和该女生的选考方案中都含有历史科目的概率;
(Ⅲ)从选考方案确定的8名男生随机选出2名,设随机变量两名男生选考方案相同时![]() ,两名男生选考方案不同时
,两名男生选考方案不同时![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面六个句子中,错误的题号是________.
①周期函数必有最小正周期;
②若![]() 则
则![]() ,
,![]() 至少有一个为
至少有一个为![]() ;
;
③![]() 为第三象限角,则
为第三象限角,则![]() ;
;
④若向量![]() 与
与![]() 的夹角为锐角,则
的夹角为锐角,则![]() ;
;
⑤存在![]() ,
,![]() ,使
,使![]() 成立;
成立;
⑥在![]() 中,O为
中,O为![]() 内一点,且
内一点,且![]() ,则O为
,则O为![]() 的重心.
的重心.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分别直方图.
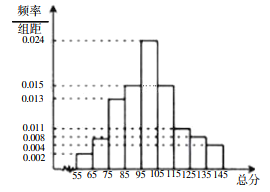
(1)求这100份数学试卷成绩的中位数;
(2)从总分在![]() 和
和![]() 的试卷中随机抽取2份试卷,求抽取的2份试卷中至少有一份总分少于65分的概率.
的试卷中随机抽取2份试卷,求抽取的2份试卷中至少有一份总分少于65分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() :
: ![]() 满足:
满足: ![]() .记
.记![]() 的前
的前![]() 项和为
项和为![]() ,并规定
,并规定![]() .定义集合
.定义集合![]() ,
, ![]()
![]() ,
, ![]() .
.
(Ⅰ)对数列![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求集合
,求集合![]() ;
;
(Ⅱ)若集合![]() ,
, ![]() ,证明:
,证明: ![]() ;
;
(Ⅲ)给定正整数![]() .对所有满足
.对所有满足![]() 的数列
的数列![]() ,求集合
,求集合![]() 的元素个数的最小值.
的元素个数的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,动圆
,动圆![]() 与圆
与圆![]() 内切且与圆
内切且与圆![]() 外切.
外切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知![]() 与
与![]() 为平面内的两个定点,过
为平面内的两个定点,过![]() 点的直线
点的直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用适当的方法表示下列集合:
(1)一年中有31天的月份的全体;
(2)大于![]() 小于12.8的整数的全体;
小于12.8的整数的全体;
(3)梯形的全体构成的集合;
(4)所有能被3整除的数的集合;
(5)方程![]() 的解组成的集合;
的解组成的集合;
(6)不等式![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com