
已知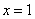 是函数
是函数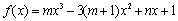 的一个极值点,其中
的一个极值点,其中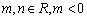 ,
,
(I)求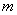 与
与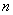 的关系式;(II)求
的关系式;(II)求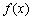 的单调区间; (III)当
的单调区间; (III)当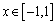 时,函数
时,函数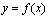 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3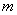 ,求
,求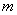 的取值范围.
的取值范围.
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
从某大学中随机抽取8名女大学生, 其身高和体重数据如表所示.
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 身高/cm | 165 | 165 | 157 | 170 | 175 | 165 | 155 | 170 |
| 体重/kg | 48 | 57 | 50 | 54 | 64 | 61 | 43 | 59 |
已知该大学某女大学生身高为165.25cm, 则预报其体重合理值为 kg.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com