
| A. | $\frac{{5\sqrt{3}}}{3}$ | B. | $\frac{{7\sqrt{3}}}{3}$ | C. | $\frac{{8\sqrt{3}}}{3}$ | D. | $3\sqrt{3}$ |
分析 利用抛物线的定义,求出A,B的坐标,再计算△AMB的面积.
解答  解:抛物线$x=\frac{1}{4}{y^2}$即为y2=4x的准线l:x=-1.
解:抛物线$x=\frac{1}{4}{y^2}$即为y2=4x的准线l:x=-1.
∵|AF|=3,
∴点A到准线l:x=-1的距离为4,
∴1+xA=4,
∴xA=3,
∴yA=±2$\sqrt{3}$,
不妨设A(3,2$\sqrt{3}$),
∴S△AFM=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$,
∵F(1,0),
∴直线AB的方程为y=$\sqrt{3}$(x-1),
∴$\left\{\begin{array}{l}{y=\sqrt{3}(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,
解得B($\frac{1}{3}$,-$\frac{2\sqrt{3}}{3}$),
∴S△BFM=$\frac{1}{2}$×2×$\frac{2\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$,
∴S△AMB=S△AFM+S△BFM=2$\sqrt{3}$+$\frac{2\sqrt{3}}{3}$=$\frac{8\sqrt{3}}{3}$,
故选:C
点评 本题考查抛物线的定义,考查三角形的面积的计算,确定A,B的坐标是解题的关键.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\frac{2}{e}$ | B. | $\frac{1}{2}$+$\frac{2}{e}$ | C. | 1+$\frac{1}{e}$ | D. | $\frac{1}{2}$+$\frac{1}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
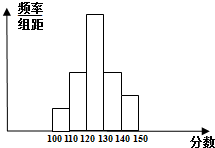 为了了解学生的数学复习情况,某校从第四次模拟考试成绩中抽取一个样本,将样本分成5组,绘成频率分布直方图,图中从左到右小矩形面积之比为2:5:10:5:3,最左边一组的频数为4,请结合直方图解决下列问题.
为了了解学生的数学复习情况,某校从第四次模拟考试成绩中抽取一个样本,将样本分成5组,绘成频率分布直方图,图中从左到右小矩形面积之比为2:5:10:5:3,最左边一组的频数为4,请结合直方图解决下列问题.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-4)∪[3,4) | B. | (-4,-2]∪[3,4) | C. | (-∞,-2]∪[3,+∞) | D. | (-∞,-2]∪(4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k=2,b=3 | B. | k=-2,b=3 | C. | k=1,b=1 | D. | k=-1,b=3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com