
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
分析 利用直线AB与抛物线相交,求A,B出的坐标,写求出直线AC和C的坐标.易得直线CF与AB关于x轴对称.
所以AD与BE关于x轴对称,所以xD=xE,且G点在x轴上.G到直线AB的距离d1,点C到直线AB的距离d2,则$\frac{{{S_{△ABC}}}}{{{S_{△ABG}}}}$=$\frac{{d}_{1}}{{d}_{2}}$即可得到答案.
解答  解:直线AB过抛物线的焦点F且与抛物线交于A,B两点,
解:直线AB过抛物线的焦点F且与抛物线交于A,B两点,
则有$\left\{\begin{array}{l}{{y}^{2}=2px}\\{y=x+\frac{p}{2}}\end{array}\right.$,解得A(,$(\sqrt{2}+\frac{3}{2})P$,$(\sqrt{2}+1)P$),B($(\sqrt{2}-1)P$,$(\sqrt{2}-\frac{1}{2})P$)
过A点作抛物线的切线与抛物线的准线交于C点,可得:C($-\frac{P}{2}$,P)
∴直线CF:$y=-(x-\frac{p}{2})$
易得直线CF与AB关于x轴对称.
所以AD与BE关于x轴对称,所以xD=xE,且G点在x轴上.
xD=xE=$(\frac{3}{2}-\sqrt{2})P$,${y}_{D}=(\sqrt{2}-1)P$.
直线AD的方程为:$y-(\sqrt{2}-)P=\frac{\sqrt{2}}{2}[x-(\sqrt{2}-\frac{3}{2})P]$,与y=0联立解得x=-$\frac{P}{2}$,
所以:点G到直线AB的距离d1=$\frac{p}{\sqrt{2}}$
点C到直线AB的距离d2=|CF|=$\sqrt{2}P$;
因此:$\frac{{{S_{△ABC}}}}{{{S_{△ABG}}}}$=$\frac{{d}_{1}}{{d}_{2}}$=2,
故选:C.
点评 本题考查了抛物线的性质的运用,抛物线的特性(对称轴性)的运用能力和计算能力,综合性强,属于难题.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{5\sqrt{3}}}{3}$ | B. | $\frac{{7\sqrt{3}}}{3}$ | C. | $\frac{{8\sqrt{3}}}{3}$ | D. | $3\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
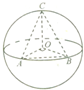 如图所示,已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的半径为( )
如图所示,已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的半径为( )| A. | 6 | B. | 8 | C. | 36 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
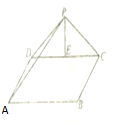 如图所示,在空间四边形ABCD中,AD、CD、AB、BD的中点分别为E、F、G、H.已知AD=1,BC=$\sqrt{3}$,且,对角线$BD=\frac{{\sqrt{13}}}{2},AC=\frac{{\sqrt{3}}}{2}$.求证:△EFG为直角三角形.
如图所示,在空间四边形ABCD中,AD、CD、AB、BD的中点分别为E、F、G、H.已知AD=1,BC=$\sqrt{3}$,且,对角线$BD=\frac{{\sqrt{13}}}{2},AC=\frac{{\sqrt{3}}}{2}$.求证:△EFG为直角三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | 2 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com