练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
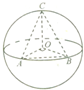
    7．如图所示，已知A，B是球O的球面上两点，∠AOB=90°，C为该球面上的动点，若三棱锥O-ABC体积的最大值为36，则球O的半径为（　　）
    A．6B．8C．36D．64

    分析 当点C位于垂直于面AOB的直径端点时，三棱锥O-ABC的体积最大，利用三棱锥O-ABC体积的最大值为36，即可求出半径．

    解答 解：如图所示，当点C位于垂直于面AOB的直径端点时，三棱锥O-ABC的体积最大，设球O的半径为R，此时VO-ABC=VC-AOB=$\frac{1}{3}×\frac{1}{2}×{R}^{2}×R$=36，
    故R=6，
    故选A．

    点评 本题考查球的半径，考查体积的计算，确定点C位于垂直于面AOB的直径端点时，三棱锥O-ABC的体积最大是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    17．集合A={x||x-2|+|x+1|≥5}，B=$\left\{{x|\frac{16}{x}＞x}\right\}$，则A∩B=（　　）
    A．（-∞，-4）∪[3，4）B．（-4，-2]∪[3，4）C．（-∞，-2]∪[3，+∞）D．（-∞，-2]∪（4，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．在平面直角坐标系中，定义d（P1，P2）=max{|x1-x2|，|y1-y2|}为两点P1（x1，y1），P2（x2，y2）的“切比雪夫距离”，则点P（3，1）到直线y=2x-1上一点的“切比雪夫距离”的最小值为$\frac{4}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．某餐饮业培训学校对男、女各20名学员进行考评，考评成绩（满分100分）如茎叶图所示：
    （I）若大于或等于80分为优秀学员，80分以下为非优秀学员，根据茎叶图填写2×2列联表，并判断能否有95%的把握认为学员的优秀与性别有关？
    非优秀优秀总数
    男20
    女20
    总数40
    （Ⅱ）若从考评成绩95分以上（包括95分）的学员中任选两人代表学校参加上一级单位举办的服务比赛，求至少有一名男学员参加的概率．
    下面的临界值表供参考：
     P（K2≥k） 0.15 0.10 0.05 0.025 0.010 0.005 0.001
     k 2.072 2.706 3.841 5.024 6.635 7.879 10.828
    （参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$）n=a+b+c+d．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知抛物线y2=2px（p＞0），倾斜角为$\frac{π}{4}$的直线AB过抛物线的焦点F且与抛物线交于A，B两点（|AF|＞|BF|）．过A点作抛物线的切线与抛物线的准线交于C点，直线CF交抛物线于D，E两点（|DF|＜|FE|）．直线AD，BE相交于G，则$\frac{{{S_{△ABC}}}}{{{S_{△ABG}}}}$=（　　）
    A．$\sqrt{2}$B．$\sqrt{3}$C．2D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．求平行于直线2x-y+10=0且与两坐标轴围成的三角形的面积为9的直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知△ABC的角A、B、C的对边分别为a、b、c，其面积$S=4\sqrt{3}$，∠B=60°，且a2+c2=2b2；等差数列{an}中，且a1=a，公差d=b．数列{bn}的前n项和为Tn，且Tn-2bn+2=0，n∈N*．
    （1）求数列{an}、{bn}的通项公式；
    （2）设${c_n}=\left\{{\begin{array}{l}{{a_n}，n为奇数}\\{{b_n}\;\;，n为偶数}\end{array}}\right.$，求数列{cn}的前2n+1项和T2n+1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．在△ABC中，a+b+10c=2（sinA+sinB+10sinC），A=60°，则a=$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．一个几何体的三视图如图所示，正视图与侧视图为全等的矩形，俯视图为正方形，则该几何体的表面积为28+4$\sqrt{10}$；体积为8．

    查看答案和解析>>

    同步练习册答案