
分析 (1)利用a2+c2=2b2,所以b2=2accosB=16,即b=4,再求出a,可得数列{an}的通项公式;利用Tn-2bn+2=0,再写一式,相减,可得数列{bn}是以2为首项,公比为2的等比数列,即可得出数列{bn}的通项公式;
(2)利用分组求和,即可求数列{cn}的前2n+1项和T2n+1.
解答 解:(1)因为$S=4\sqrt{3}$,∠B=60°,所以ac=16,
由于a2+c2=2b2,所以b2=2accosB=16,即b=4,
所以a2+c2=2b2=32,解得a=4,
所以an=4n;
由于Tn-2bn+2=0,所以当n≥2时Tn-1-2bn-1+2=0
相减整理的$\frac{b_n}{{{b_{n-1}}}}=2$,即数列{bn}是以2为首项,公比为2的等比数列,
即${b_n}={2^n}$;
(2)T2n+1=c1+c2+…+c2n+1=(a1+a3+…a2n+1)+(b2+b4+…b2n)
=$\frac{{({n+1})({4+8n+4})}}{2}+\frac{{4({1-{4^n}})}}{1-4}$=$4{({n+1})^2}+\frac{4}{3}({{4^n}-1})$
点评 本题考查数列的通项与求和,考查学生的计算能力,确定数列的通项是关键.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 1 | C. | $\sqrt{3}$i | D. | i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
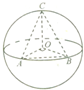 如图所示,已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的半径为( )
如图所示,已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的半径为( )| A. | 6 | B. | 8 | C. | 36 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
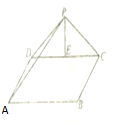 如图所示,在空间四边形ABCD中,AD、CD、AB、BD的中点分别为E、F、G、H.已知AD=1,BC=$\sqrt{3}$,且,对角线$BD=\frac{{\sqrt{13}}}{2},AC=\frac{{\sqrt{3}}}{2}$.求证:△EFG为直角三角形.
如图所示,在空间四边形ABCD中,AD、CD、AB、BD的中点分别为E、F、G、H.已知AD=1,BC=$\sqrt{3}$,且,对角线$BD=\frac{{\sqrt{13}}}{2},AC=\frac{{\sqrt{3}}}{2}$.求证:△EFG为直角三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2005 | B. | 2006 | C. | 2007 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | 2 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}+{y}^{2}$=1 | B. | $\frac{{x}^{2}}{9}+\frac{{y}^{2}}{81}$=1 | ||
| C. | $\frac{{x}^{2}}{9}+{y}^{2}$=1或 $\frac{{x}^{2}}{9}+\frac{{y}^{2}}{81}$=1 | D. | $\frac{{x}^{2}}{81}+\frac{{y}^{2}}{9}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com