
分析 设点Q是直线y=2x-1上一点,且Q(x,2x-1),可得d(P,Q)=max{|x-3|,|2-2x|},讨论|x-3|,|2-2x|的大小,可得距离d,再由函数的性质,可得最小值.
解答 解:设点Q是直线y=2x-1上一点,且Q(x,2x-1),可得d(P,Q)=max{|x-3|,|2-2x|},
由|x-3|≥|2-2x|,解得-1≤x≤$\frac{5}{3}$,即有d(P,Q)=|x-3|,
当x=$\frac{5}{3}$时,取得最小值$\frac{4}{3}$;
由|x-3|<|2-2x|,解得x>$\frac{5}{3}$或x<-1,即有d(P,Q)=|2x-2|,
d(P,Q)的范围是(3,+∞)∪($\frac{4}{3}$,+∞)=($\frac{4}{3}$,+∞).无最值,
综上可得,P,Q两点的“切比雪夫距离”的最小值为$\frac{4}{3}$.
故答案是:$\frac{4}{3}$.
点评 本题考查新定义的理解和运用,考查点到直线的距离,属于中档题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:解答题
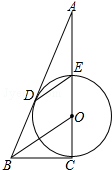 如图,CE是⊙O的直径,BD切⊙O于点D,DE∥BO,CE的延长线交BD于点A
如图,CE是⊙O的直径,BD切⊙O于点D,DE∥BO,CE的延长线交BD于点A查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 1 | C. | $\sqrt{3}$i | D. | i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,2x2-1≤0 | B. | ?x∉R,2x2-1≤0 | C. | ?x∈R,2x2-1≤0 | D. | ?x∉R,2x2-1≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
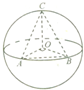 如图所示,已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的半径为( )
如图所示,已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的半径为( )| A. | 6 | B. | 8 | C. | 36 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}+{y}^{2}$=1 | B. | $\frac{{x}^{2}}{9}+\frac{{y}^{2}}{81}$=1 | ||
| C. | $\frac{{x}^{2}}{9}+{y}^{2}$=1或 $\frac{{x}^{2}}{9}+\frac{{y}^{2}}{81}$=1 | D. | $\frac{{x}^{2}}{81}+\frac{{y}^{2}}{9}$=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com