
分析 可根据an=f(2n)再利用对于任意的x,y∈R,都有f(x•y)=xf(y)+yf(x)成立令x=2n,y=2得到递推关系式an+1=2an+2×2n然后两边同除以2n+1可构造出数列{$\frac{{a}_{n}}{{2}^{n}}$}是以 $\frac{{a}_{1}}{2}$=1为首项公差为1的等差数列后就可解决问题了.
解答 解:由于an=f(2n)则an+1=f(2n+1)且a1=2=f(2)
∵对于任意的x,y∈R,都有f(x•y)=xf(y)+yf(x)
∴令x=2n,y=2则f(2n+1)=2nf(2)+2f(2n)
∴an+1=2an+2×2n
∴$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{{a}_{n}}{{2}^{n}}$=1
∴数列{ $\frac{{a}_{n}}{{2}^{n}}$}是以$\frac{{a}_{1}}{2}$=1为首项公差为1的等差数列
∴${S_n}=(n-1){2^{n+1}}+2$.
点评 此题主要考查了利用函数的特征求数列的通项公式,是函数与数列的综合题.解题的关键是分别赋予x=2n,y=2得到an+1=2an+2×2n然后构造出数列数列{ $\frac{{a}_{n}}{{2}^{n}}$}是以 $\frac{{a}_{1}}{2}$=1为首项公差为1的等差数列后就可求解.同时要对递推关系式an+1=pan+qn通过两边同除以qn+1构造出{$\frac{{a}_{n}}{{q}^{n}}$}为等差数列进而求出an的通项公式.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:解答题
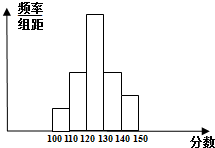 为了了解学生的数学复习情况,某校从第四次模拟考试成绩中抽取一个样本,将样本分成5组,绘成频率分布直方图,图中从左到右小矩形面积之比为2:5:10:5:3,最左边一组的频数为4,请结合直方图解决下列问题.
为了了解学生的数学复习情况,某校从第四次模拟考试成绩中抽取一个样本,将样本分成5组,绘成频率分布直方图,图中从左到右小矩形面积之比为2:5:10:5:3,最左边一组的频数为4,请结合直方图解决下列问题.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-3,1,\sqrt{6}})$和$({3,-1,-\sqrt{6}})$ | B. | $({-\frac{3}{4},\frac{1}{4},\frac{{\sqrt{6}}}{4}})$ | ||
| C. | $({-\frac{3}{4},\frac{1}{4},\frac{{\sqrt{6}}}{4}})$和$({\frac{3}{4},-\frac{1}{4},-\frac{{\sqrt{6}}}{4}})$ | D. | $({3,-1,-\sqrt{6}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com