
分析 根据向量$\overrightarrow{z}$与$\overrightarrow{a}$共线,设出$\overrightarrow{z}$=λ$\overrightarrow{a}$,代入数量积$\overrightarrow{a}$•$\overrightarrow{z}$=-18,即可求出λ的值.
解答 解:由向量$\overrightarrow{z}$与向量$\overrightarrow{a}$共线,且$\overrightarrow{a}$=(2,-1,2),
设$\overrightarrow{z}$=λ$\overrightarrow{a}$=(2λ,-λ,2λ),
由$\overrightarrow{a}$•$\overrightarrow{z}$=-18,
得2×2λ-1×(-λ)+2×2λ=-18,
解得λ=-2,
所以$\overrightarrow{z}$=(-4,2,-4).
故答案为:(-4,2,-4).
点评 本题考查了空间向量的共线定理和数量积运算问题,是基础题目.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 6$\frac{2}{3}$ | C. | 4 | D. | 5$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{5\sqrt{3}}}{3}$ | B. | $\frac{{7\sqrt{3}}}{3}$ | C. | $\frac{{8\sqrt{3}}}{3}$ | D. | $3\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,圆O和圆O′都经过点A和点B,PQ切圆O于点P,交圆O′于Q,M,交AB的延长线于N.若PN=2,MN=1,则MQ等于( )
如图,圆O和圆O′都经过点A和点B,PQ切圆O于点P,交圆O′于Q,M,交AB的延长线于N.若PN=2,MN=1,则MQ等于( )| A. | $\frac{7}{2}$ | B. | 3 | C. | $\sqrt{10}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 1 | C. | $\sqrt{3}$i | D. | i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4+2b+c=0 | B. | b<0,c>0 | ||
| C. | (x1-1)(x2-1)(x3-1)(x4-1)(x5-1)=0 | D. | x1+x2+x3+x4+x5=10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
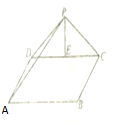 如图所示,在空间四边形ABCD中,AD、CD、AB、BD的中点分别为E、F、G、H.已知AD=1,BC=$\sqrt{3}$,且,对角线$BD=\frac{{\sqrt{13}}}{2},AC=\frac{{\sqrt{3}}}{2}$.求证:△EFG为直角三角形.
如图所示,在空间四边形ABCD中,AD、CD、AB、BD的中点分别为E、F、G、H.已知AD=1,BC=$\sqrt{3}$,且,对角线$BD=\frac{{\sqrt{13}}}{2},AC=\frac{{\sqrt{3}}}{2}$.求证:△EFG为直角三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com