
| A. | 4+2b+c=0 | B. | b<0,c>0 | ||
| C. | (x1-1)(x2-1)(x3-1)(x4-1)(x5-1)=0 | D. | x1+x2+x3+x4+x5=10 |
分析 先根据一元二次方程根的情况可判断f(2)一定是一个解,再假设f(x)的一解为A可得到x1+x2=4,同理可得到x3+x4=4,进而可得到x1+x2+x3+x4+x5=10,即可得到最后答案.
解答 解:函数h(x)=f2(x)+bf(x)+c,对于f2(x)+bf(x)+c=0来说,f(x)最多只有2解,
又f(x)=$\frac{1}{|x-2|}$(x≠2),函数关于x=2对称,当x不等于2时,x最多四解.
而题目要求5解,即可推断f(2)为一解,
假设f(x)的另一个解为A,得f(x)=$\frac{1}{|x-2|}$=A;
根据函数y═$\frac{1}{|x-2|}$的对称性得出:x1=2+A,x2=2-A,x1+x2=4;
同理:x3+x4=4;
所以:x1+x2+x3+x4+x5=4+4+2=10;
故选:D.
点评 本题主要考查一元二次方程根的情况和含有绝对值的函数的解法,考查基础知识的综合运用能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
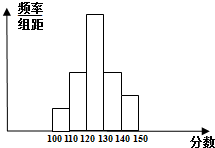 为了了解学生的数学复习情况,某校从第四次模拟考试成绩中抽取一个样本,将样本分成5组,绘成频率分布直方图,图中从左到右小矩形面积之比为2:5:10:5:3,最左边一组的频数为4,请结合直方图解决下列问题.
为了了解学生的数学复习情况,某校从第四次模拟考试成绩中抽取一个样本,将样本分成5组,绘成频率分布直方图,图中从左到右小矩形面积之比为2:5:10:5:3,最左边一组的频数为4,请结合直方图解决下列问题.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k=2,b=3 | B. | k=-2,b=3 | C. | k=1,b=1 | D. | k=-1,b=3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com