
分析 (I)由绝对值不等式的性质,求得f(x)的最小值,令m不小于最小值,即可得到所求M;
(Ⅱ)由题意可得1=$\frac{1}{4}$(3a+b),运用乘1法和基本不等式,即可得证.
解答 解:(I)函数f(x)=|2x+1|+|2x-3|,
可得|2x+1|+|2x-3|≥|(2x+1)-(2x-3)|=4,
当(2x+1)(2x-3)≤0,即-$\frac{1}{2}$≤x≤$\frac{3}{2}$时,f(x)取得最小值4.
由题意可得m≥4,
即实数m的最小值M=4;
(Ⅱ)证明:正数a,b满足3a+b=4,
即1=$\frac{1}{4}$(3a+b),
$\frac{3}{b}$+$\frac{1}{a}$=$\frac{1}{4}$($\frac{3}{b}$+$\frac{1}{a}$)(3a+b)=$\frac{1}{4}$(3+3+$\frac{b}{a}$+$\frac{9a}{b}$)
≥$\frac{1}{4}$×(6+2$\sqrt{\frac{b}{a}•\frac{9a}{b}}$)=$\frac{1}{4}$×(6+2×3)=3,
当且仅当b=3a=2时,取得等号.
则$\frac{3}{b}$+$\frac{1}{a}$≥3.
点评 本题考查绝对值不等式的性质的运用:求最值,考查存在性问题的解法,以及基本不等式的运用,注意运用乘1法和满足的条件:一正二定三等,考查化简整理的运算能力,属于中档题.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,$\frac{4}{5}$) | C. | (0,1) | D. | (0,$\frac{4}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知函数f(x)的定义域为[-1,5],部分对应值如下表:
已知函数f(x)的定义域为[-1,5],部分对应值如下表:| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
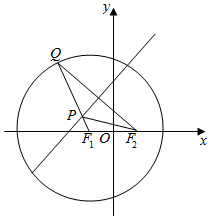 已知圆F1:(x+2)2+y2=32,点F2(2,0),点Q在圆F1上运动,QF2的垂直平分线交QF1于点P.
已知圆F1:(x+2)2+y2=32,点F2(2,0),点Q在圆F1上运动,QF2的垂直平分线交QF1于点P.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com