
分析 (1)设A(x0,y0),则B(x0,-y0),求出$\overrightarrow{TA}$,$\overrightarrow{TB}$,推出向量的数量积的表达式,利用二次函数求解最小值,然后求出A的坐标,推出抛物线方程.
(2)设M(x1,y1),由A(x0,y0),求出P的坐标,Q的坐标,求出|OP|•|OQ|的表达式,利用M(x1,y1),A(x0,y0)均在椭圆上,化简求解即可得到|OP|•|OQ|=4.
解答 解:(1)由抛物线与椭圆关于x轴对称可得:M,N关于x轴对称.
设A(x0,y0),则B(x0,-y0),且有$\frac{x_0^2}{4}+y_0^2=1$
由T(2,0)可得:$\overrightarrow{TA}=({{x_0}-2,{y_0}}),\overrightarrow{TB}=({{x_0}-2,-{y_0}})$,
∴$\overrightarrow{TA}•\overrightarrow{TB}={({{x_0}-2})^2}-y_0^2={({{x_0}-2})^2}+\frac{x_0^2}{4}-1$=$\frac{5}{4}x_0^2-4{x_0}+3=\frac{5}{4}{({{x_0}-\frac{8}{5}})^2}-\frac{1}{5}$…(3分)
因为A在右半椭圆上(非长轴顶点)∴0<x0<2∴${x_0}=\frac{8}{5}$时,
${({\overrightarrow{TA}•\overrightarrow{TB}})_{min}}=-\frac{1}{5}$,将${x_0}=\frac{8}{5}$代入可得${y_0}=\frac{3}{5}$
即A($\frac{8}{5}$,$\frac{3}{5}$),代入到抛物线方程可得:a=$\frac{9}{40}$,
所以此时抛物线C2的方程为${y^2}=\frac{9}{40}x$.…(5分)
(2)设M(x1,y1),由A(x0,y0)可得:${k_{MA}}=\frac{{{y_1}-{y_0}}}{{{x_1}-{x_0}}}$
∵MA的方程为:y-y1=$\frac{{y}_{1}-{y}_{0}}{{x}_{1}-{x}_{0}}(x-{x}_{1})$
令y=0,可解得:${x_P}=\frac{{{x_0}{y_1}-{x_1}{y_0}}}{{{y_1}-{y_0}}}$
同理可解得MB与x轴的交点Q的横坐标${x_Q}=\frac{{{x_0}{y_1}+{x_1}{y_0}}}{{{y_1}+{y_0}}}$…(7分)
所以$|{OP}|•|{OQ}|=|{{x_P}{x_Q}}|=|{\frac{{{x_0}{y_1}-{x_1}{y_0}}}{{{y_1}-{y_0}}}•\frac{{{x_0}{y_1}+{x_1}{y_0}}}{{{y_1}+{y_0}}}}|=|{\frac{x_0^2y_1^2-x_1^2y_0^2}{y_1^2-y_0^2}}|$①
因为M(x1,y1),A(x0,y0)均在椭圆上
∴$\left\{\begin{array}{l}\frac{x_0^2}{4}+y_0^2=1\\ \frac{x_1^2}{4}+y_1^2=1\end{array}\right.⇒\left\{\begin{array}{l}x_0^2=4-4y_0^2\\ x_1^2=4-4y_1^2\end{array}\right.$,代入到①可得:…(10分)$|{OP}|•|{OQ}|=|{\frac{x_0^2y_1^2-x_1^2y_0^2}{y_1^2-y_0^2}}|=|{\frac{{({4-4y_0^2})y_1^2-({4-4y_1^2})y_0^2}}{y_1^2-y_0^2}}|=|{\frac{4y_1^2-4y_0^2}{y_1^2-y_0^2}}|=4$
所以|OP|•|OQ|=4,即为定值…(12分)
点评 本题考查抛物线的求法,数量积的应用,直线与椭圆的位置关系的综合应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{2}$)及(0,$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,0)及($\frac{1}{2}$,+∞) | C. | (0,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
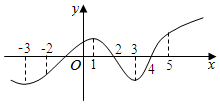
| A. | 在区间(1,3)内f(x)是减函数 | B. | 当x=1时,f(x)取到极大值 | ||
| C. | 在(4,5)内f(x)是增函数 | D. | 当x=2时,f(x)取到极小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
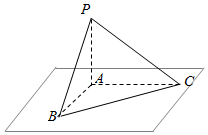 三棱锥P-ABC中,PA⊥平面ABC,PA=3,AC=4,PB=PC=BC.
三棱锥P-ABC中,PA⊥平面ABC,PA=3,AC=4,PB=PC=BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com