
分析 (1)对函数求导,结合f′(x)>0,f′(x)<0,f′(x)=0可求解
(2)由题意可得-a≤-x2+4ax-3a2≤a在[1-a,1+a]恒成立,结合二次函数的对称轴x=2a与区间[1-a,1+a]与的位置分类讨论进行求解.
解答 解:(1)f′(x)=-3x2+12ax-9a2,且0<a<1,
当f′(x)>0时,得a<x<3a;
当f′(x)<0时,得x<a或x>3a;
∴f(x)的单调递增区间为(a,3a);
f(x)的单调递减区间为(-∞,a)和(3a,+∞).
(2)f′(x)=-3x2+12ax-9a2=3[-(x-2a)2+a2],
令g(x)=-(x-2a)2+a2,
①当2a≤1-a时,即0<a≤$\frac{1}{3}$时,f′(x)在区间[1-a,1+a]内单调递减.
∴[g(x)]max=g(1-a)=-24a2+18a-3,[g(x)]min=f′(1+a)=6a-3.
∵|f′(x)|≤3a,
∴-a≤g(x)≤a,
∴$\left\{\begin{array}{l}{-{8a}^{2}+6a-1≤a}\\{2a-1≥-a}\end{array}\right.$,
∴a≥$\frac{1}{3}$,
此时,a=$\frac{1}{3}$.
②当2a>1-a,且2a<a+1时,即$\frac{1}{3}$<a<1,[g(x)]max=g(2a)=a2.
∵-a≤g(x)≤a,
∴$\left\{\begin{array}{l}{g(1+a)≥-a}\\{g(1-a)≥-a}\\{g(2a)≤a}\end{array}\right.$,
即 $\left\{\begin{array}{l}{2a-1≥-a}\\{-{8a}^{2}+6a-1≥-a}\\{{a}^{2}≤a}\end{array}\right.$,
∴$\frac{1}{3}$≤a≤$\frac{7+\sqrt{17}}{16}$.
此时,$\frac{1}{3}$<a≤$\frac{7+\sqrt{17}}{16}$,
③当2a≥1+a时,得a≥1与已知0<a<1矛盾,
综上所述,实数a的取值范围为[$\frac{1}{3}$,$\frac{7+\sqrt{17}}{16}$].
点评 本题综合考查了函数的导数的运用及二次函数在闭区间上的最值问题,(2)的求解的关键是要对二次函数的对称轴相对区间的位置分类讨论,体现了分类讨论的思想在解题中的应用.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:选择题
| A. | [$\frac{3}{2}$,+∞) | B. | (-∞,0) | C. | (0,$\frac{3}{2}$] | D. | (0,$\frac{3}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知函数f(x)的定义域为[-1,5],部分对应值如下表:
已知函数f(x)的定义域为[-1,5],部分对应值如下表:| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
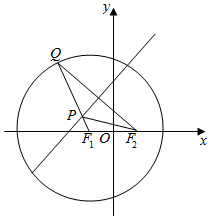 已知圆F1:(x+2)2+y2=32,点F2(2,0),点Q在圆F1上运动,QF2的垂直平分线交QF1于点P.
已知圆F1:(x+2)2+y2=32,点F2(2,0),点Q在圆F1上运动,QF2的垂直平分线交QF1于点P.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB为圆0的直径,C是圆上一点,∠ACB的平分线与圆O和AB的交点分别为D,E,点P为AB延长线上一点,且PC=PE.
如图,AB为圆0的直径,C是圆上一点,∠ACB的平分线与圆O和AB的交点分别为D,E,点P为AB延长线上一点,且PC=PE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com