
| A�� | [$\frac{3}{2}$��+�ޣ� | B�� | ��-�ޣ�0�� | C�� | ��0��$\frac{3}{2}$] | D�� | ��0��$\frac{3}{2}$�� |
���� ��������f��x�����õ�x1��x2����x=-1�Գƣ�x3x4=1�������������������ν�Ͻ�����⼴�ɣ�
���  �⣺������f��x����ͼ�����ң�
�⣺������f��x����ͼ�����ң�
�߷���f��x��=k���ĸ���ͬ�Ľ�x1��x2��x3��x4��
��x1��x2��x3��x4��
��x1��x2����x=-1�Գƣ���x1+x2=-2��
0��x3��1��x4��2��
��|log${\;}_{\frac{1}{2}}$x3|=|log${\;}_{\frac{1}{2}}$x4|��
��log${\;}_{\frac{1}{2}}$x3=-log${\;}_{\frac{1}{2}}$x4��
��log${\;}_{\frac{1}{2}}$x3+log${\;}_{\frac{1}{2}}$x4=0
��log${\;}_{\frac{1}{2}}$x3x4=0
��x3x4=1��
��|log${\;}_{\frac{1}{2}}$x|=1��x=2��$\frac{1}{2}$��
��1��x4��2��$\frac{1}{2}$��x3��1��
��$\frac{{��{x_1}+{x_2}��{x_3}}}{2}$+$\frac{1}{{x_3^2{x_4}}}$=-x3+$\frac{1}{{x}_{3}}$��$\frac{1}{2}$��x3��1��
����y=-x3+$\frac{1}{{x}_{3}}$����$\frac{1}{2}$��x3��1����������
���x3=$\frac{1}{2}$ȡ�����ֵ��Ϊy=-$\frac{1}{2}$+2=$\frac{3}{2}$��
��x3=1ʱ������ֵ��СΪy=-1+1=0��
������ȡֵ��Χ�ǣ�0��$\frac{3}{2}$]��
��ѡ��C
���� ���⿼��ֶκ��������ã���Ҫ���麯���ĵ����Ե����ã��������ν�ϵ�˼�뷽���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-$\frac{1}{2}$������0��$\frac{1}{2}$�� | B�� | ��-$\frac{1}{2}$��0������$\frac{1}{2}$��+�ޣ� | C�� | ��0��$\frac{1}{2}$�� | D�� | ��$\frac{1}{2}$��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��+�ޣ� | B�� | ��-1��1�� | C�� | ��-�ޣ�1�� | D�� | ��-�ޣ�+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
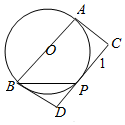 ��֪ABΪ��O��һ��ֱ������PΪԲ������AB��һ�㣬�Ե�PΪ�е�������l��ʹ��AC��l��BD��l������ֱ�ΪC��D��
��֪ABΪ��O��һ��ֱ������PΪԲ������AB��һ�㣬�Ե�PΪ�е�������l��ʹ��AC��l��BD��l������ֱ�ΪC��D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -9 | B�� | -16 | C�� | -12 | D�� | -11 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com