考点:数列与不等式的综合,数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)先利用前n项积与前(n-1)项积的关系,得到等比数列{an}的第三项的值,结合首项的值,求出通项an,然后现利用条件求出通项bn;
(Ⅱ)(i)利用数列特征进行分组求和,一组用等比数列求和公式,另一组用裂项法求和,得出本小题结论;(ii)本小题可以采用猜想的方法,得到结论,再加以证明.
解答:
解:(Ⅰ)∵a
1a
2a
3…a
n=
()bn(n∈N
*) ①,
当n≥2,n∈N
*时,
a1a2a3…an-1=()bn-1 ②,
由①②知:
an=()bn-bn-1,
令n=3,则有
a3=()b3-b2.
∵b
3=6+b
2,
∴a
3=8.
∵{a
n}为等比数列,且a
1=2,
∴{a
n}的公比为q,则
q2==4,
由题意知a
n>0,∴q>0,∴q=2.
∴
an=2n(n∈N
*).
又由a
1a
2a
3…a
n=
()bn(n∈N
*)得:
21×22×23…×2n=()bn,
2=()bn,
∴b
n=n(n+1)(n∈N
*).
(Ⅱ)(i)∵c
n=
-=
-=
-(-).
∴S
n=c
1+c
2+c
3+…+c
n=
-(-)+-(-)+…+-(-)=
++…+-(1-)=
1--1+=
-;
(ii)因为c
1=0,c
2>0,c
3>0,c
4>0;
当n≥5时,
cn=[-1],
而
-=
>0,
得
≤<1,
所以,当n≥5时,c
n<0,
综上,对任意n∈N
*恒有S
4≥S
n,故k=4.
点评:本题考查了等比数列通项公式、求和公式,还考查了分组求和法、裂项求和法和猜想证明的思想,证明可以用二项式定理,还可以用数学归纳法.本题计算量较大,思维层次高,要求学生有较高的分析问题解决问题的能力.本题属于难题.



 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案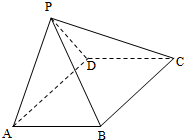 如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.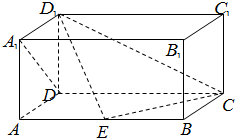 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.