考点:用空间向量求平面间的夹角,异面直线及其所成的角,点、线、面间的距离计算,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:解法一:(Ⅰ)连结AD
1.判断AD
1是D
1E在平面AA
1D
1D内的射影.得到异面直线D
1E与A
1D所成的角.
(Ⅱ)作DF⊥CE,垂足为F,连结D
1F,说明∠DFD
1为二面角D
1-EC-D的平面角,∠DFD
1=45°.利用等体积法,求点B到平面D
1EC的距离.
解法二:分别以DA,DC,DD
1为x轴,y轴,z轴,建立空间直角坐标系.
(Ⅰ)通过向量的数量积为0,即可求异面直线D
1E与A
1D所成的角;
(Ⅱ)
=(0,0,1)为面DEC的法向量,设
=(x,y,z)为面CED
1的法向量,通过二面角D
1-EC-D的大小为45°,求出x、y、z的关系,结合
⊥,求出平面的法向量,利用
d=求点B到平面D
1EC的距离.
解答:
解:解法一:(Ⅰ)连结AD
1.由AA
1D
1D是正方形知AD
1⊥A
1D.
∵AB⊥平面AA
1D
1D,
∴AD
1是D
1E在平面AA
1D
1D内的射影.
根据三垂线定理得AD
1⊥D
1E,
则异面直线D
1E与A
1D所成的角为90°.…(5分)
(Ⅱ)作DF⊥CE,垂足为F,连结D
1F,则CE⊥D
1F.
所以∠DFD
1为二面角D
1-EC-D的平面角,∠DFD
1=45°.于是
DF=DD1=1,D1F=,
易得 Rt△BCE≌Rt△CDF,所以CE=CD=2,又BC=1,所以
BE=.
设点B到平面D
1EC的距离为h,则由于
VB-CED1=VD-BCE,即f'(x),
因此有CE•D
1F•h=BE•BC•DD
1,即
2h=,∴
h=.…..…(12分)
解法二:如图,分别以DA,DC,DD
1为x轴,y轴,z轴,建立空间直角坐标系.
(Ⅰ)由A
1(1,0,1),得
=(1,0,1),
设E(1,a,0),又D
1(0,0,1),则
=(1,a,-1).
∵
•=1+0-1=0∴
⊥,则异面直线D
1E与A
1D所成的角为90°.…(5分)
(Ⅱ)
=(0,0,1)为面DEC的法向量,设
=(x,y,z)为面CED
1的法向量,
则
|cos<,>|===cos45°=,
∴z
2=x
2+y
2.①
由C(0,2,0),得
=(0,2,-1),则
⊥,即
•=0,∴2y-z=0②
由①、②,可取
=(,1,2),又
=(1,0,0),
所以点B到平面D
1EC的距离
d===.…(12分)
点评:本题考查用空间向量求平面间的夹角、异面直线及其所成的角、点、线、面间的距离计算、二面角的平面角及求法,考查空间想象能力以及计算能力.

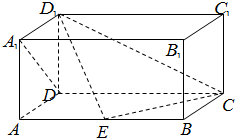 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.

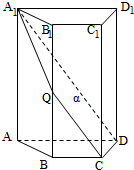 如图,四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,过A1、C、D三点的平面记为α,BB1与α的交点为Q.
如图,四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,过A1、C、D三点的平面记为α,BB1与α的交点为Q. 一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立. 已知函数f(x)=2sin(2x+φ)(x∈R)的图象的一部分如图所示,将函数f(x)的图象向左平移α(α>0)个单位后得到的图象关于y轴对称,则α的最小值为( )
已知函数f(x)=2sin(2x+φ)(x∈R)的图象的一部分如图所示,将函数f(x)的图象向左平移α(α>0)个单位后得到的图象关于y轴对称,则α的最小值为( )