
分析 利用正弦定理得出b=8sinB,根据B+C的度数和三角形只有一解,可得B只有一个值,根据正弦函数的性质得到B的范围,从而得出b的范围.
解答 解:∵A=30°,a=4,
根据正弦定理得:$\frac{a}{sinA}=\frac{b}{sinB}$,
∴b=8sinB,
又B+C=180°-30°=150°,且三角形只一解,可得B有一个值,
∴0<B≤30°,或B=90°.
∴0<sinB≤$\frac{1}{2}$,或sinB=1,
又b=8sinB,
∴b的取值范围为(0,4]∪{8}.
故答案为:(0,4]∪{8}.
点评 本题考查了正弦定理,正弦函数的性质,特殊角的三角函数值,属于中档题.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:选择题
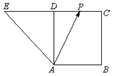 如图,四边形ABCD是正方形,延长CD至E,使得DE=CD,若点P为CD的中点,且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ=( )
如图,四边形ABCD是正方形,延长CD至E,使得DE=CD,若点P为CD的中点,且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ=( )| A. | 3 | B. | $\frac{5}{2}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{5}{2},-1})∪[2,5)$ | B. | $({-\frac{4}{3},-1}]∪[5,10)$ | C. | $[{-1,-\frac{2}{3}})∪[5,10)$ | D. | $[{-\frac{4}{3},-1}]∪[5,10)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2)或(-1,-2) | B. | (1,2)或(1,-2) | C. | (1,2) | D. | (1,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com