
���� ��1������ż������֪f��x��=f��-x����ȡx=-1���뼴�����k��ֵ��
��2���ɣ�1���н��ۣ����Եõ������Ľ���ʽ�����캯��y=log4��4x+1��-x�������������ĵ����Լ�ֵ���ݺ��������ж�������������ȷ��bȡ��ֵͬʱ�������������������õ��𰸣�
��3������ת��Ϊy=t2+mt��t��[1��3]����СֵΪ0���������ۣ��������m��ֵ��
��� �⣺��1����f��x��=log4��4x+1��+kx��k��R����ͼ�����y��Գƣ�
�ຯ��f��x����ż������
��f��-x��=f��x��
��log4��4-x+1��-kx=log4��4x+1��+kx
��log4��4x+1��-��k+1��x=log4��4x+1��+kx
��2k+1=0
��k=-$\frac{1}{2}$��
֤������2���ɣ�1����f��x��=log4��4x+1��=-$\frac{1}{2}$x��
��y=log4��4x+1��-x-a
����y=log4��4x+1��-x-aΪ���������Һ�Ϊ����
�ʵ�a��0ʱ��y=log4��4x+1��-x-a��Ψһ����㣬
��ʱ����y=f��x����ͼ����ֱ��y=$\frac{1}{2}$x+a��һ�����㣬
��a��0ʱ��y=log4��4x+1��-x-aû����㣬
��ʱ����y=f��x����ͼ����ֱ��y=$\frac{1}{2}$x+aû�н��㣬
����������a��0ʱ������y=f��x����ͼ����ֱ��y=$\frac{1}{2}$x+aû�н��㣻
��3��h��x��=4${\;}^{f��x��+\frac{1}{2}x}$+m•2x-1=4x+m-2x��x��[0��log23]
��t=2x����t��[1��3]
��y=t2+mt��t��[1��3]����СֵΪ0
�֡�y=��t+$\frac{m}{2}$��2-$\frac{{m}^{2}}{4}$��t��[1��3]��
��-$\frac{m}{2}$��1 ��m��-2ʱ��t=1ʱymin=m+1=0��
��m=-1�����ϣ�
��-1��-$\frac{m}{2}$��3 ��-6��m��-2ʱ��t=-$\frac{m}{2}$ʱ��ymin=-$\frac{{m}^{2}}{4}$=0
��m=0 ������
��-$\frac{m}{2}$��3 ��m��-6ʱ��t=3ʱ��ymin=9+3m=0��
��m=-3�����ϣ�
��������m��ֵΪ-3��-1��
���� ������Ҫ������ż���������ʣ��Լ���������ͼ�������ʵ��ۺ�Ӧ�ã�ͬʱ�����˷������۵�˼�룬�����ۺϿ����˶���������ѵ㣬�������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����x�Ķ��κ���f��x��=ax2-4bx+1��
��֪����x�Ķ��κ���f��x��=ax2-4bx+1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | -i | C�� | 1 | D�� | i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
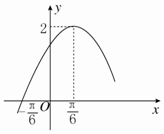 ����f��x��=Asin����x+�գ���x��R��A��0���أ�0��0���գ�$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ��
����f��x��=Asin����x+�գ���x��R��A��0���أ�0��0���գ�$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=-x | B�� | y=3|x| | C�� | y=x0��x��0�� | D�� | y=x2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com