
| ʱ�� | ��һ�� | �ڶ��� | ������ | ������ | ������ |
| ���� | 13980 | 15456 | 17890 | 19012 | 21009 |
���� ��������õ���1��2��3��Ľ����������0.3+$\frac{x-1000}{2000}$��0.1����4��5��Ľ����������2��0.3+$\frac{x-1000}{2000}$��0.1����
��� �⣺��Ϊÿ2000������0.1Ԫ�������������x-1000����2000����������
������ã���1����������0.3+$\frac{13000-1000}{2000}$��0.1=0.9��Ԫ����
��2����������0.3+$\frac{15000-1000}{2000}$��0.1=1.0��Ԫ����
��3����������0.3+$\frac{17000-1000}{2000}$��0.1=1.1��Ԫ����
��4����������2����0.3+$\frac{19000-1000}{2000}$��0.1��=2.4��Ԫ����
��5����������2����0.3+$\frac{21000-1000}{2000}$��0.1��=2.6��Ԫ����
������5��ĺ������Ϊ��0.9+1.0+1.1+2.4+2.6=8.0��Ԫ����
�ʴ��ǣ�1.1��8.0��
���� ���⿼���˵ȱ����е�ǰn��ͣ�����ʱ��ע�⡰ÿ����·ǰ1000������0.3Ԫ�����֮��ÿ2000������0.1Ԫ��������ṩ�����������������ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=$\sqrt{x}$ | B�� | y=$\frac{1}{x-1}$ | C�� | y=log0.5x | D�� | y=ex |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
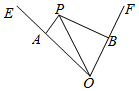 ��ͼ����һ���ڡ�EOF=60���V����ͷ��λ��P���һ�Ҵ��ϣ�Ҫ�뵽��O���ϰ����������ַ�����
��ͼ����һ���ڡ�EOF=60���V����ͷ��λ��P���һ�Ҵ��ϣ�Ҫ�뵽��O���ϰ����������ַ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com