
| A. | ①② | B. | ①④ | C. | ①②③ | D. | ②③ |
分析 △ABC中,当A为锐角时,a<bsin A,无解.当A为钝角或直角时,a≤b,无解,当bsinA<a<b时,三角形有两个解,利用正弦定理,正弦函数的图象和性质逐一判断即可得解.
解答 解:①b=3,c=4,B=30°;
有:csinB=4×$\frac{1}{2}$=2<b<c,三角形有两解,符合条件;
②b=12,c=9,C=60°;
由正弦定理可得:sinB=$\frac{bsinC}{c}$=$\frac{12×\frac{\sqrt{3}}{2}}{9}$=$\frac{2\sqrt{3}}{3}$>1,三角形无解,不符合条件;
③$b=3\sqrt{3}$,c=6,B=60°;
由正弦定理可得:sinC=$\frac{csinB}{b}$=$\frac{6×\frac{\sqrt{3}}{2}}{3\sqrt{3}}$=1,C为直角,由c<b,可得三角形无解,不符合条件;
④a=5,b=8,A=30°.
可得:bsinA=4<a<b,三角形有两解,符合条件;
故选:B.
点评 本题主要考查了正弦定理在解三角形中的应用,考查了转化思想和数形结合思想,属于中档题.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
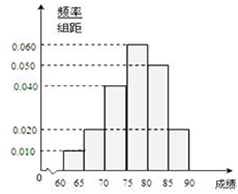 在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,得到40名考生,统计他们的成绩,得到如图所示的频率分布直方图:
在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,得到40名考生,统计他们的成绩,得到如图所示的频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相离 | B. | 外切 | C. | 内切 | D. | 相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com