
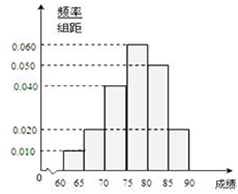
 在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,得到40名考生,统计他们的成绩,得到如图所示的频率分布直方图:
在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,得到40名考生,统计他们的成绩,得到如图所示的频率分布直方图:分析 (1)根据系统抽样的定义可得,用的是系统抽样.
(2)根据频率=$\frac{频率}{组距}×组距$求解;
(3)根据众数是频率分布直方图中最高矩形的宽的中点横坐标,中位数所在的垂直于横轴的直线平分所有矩形的面积,求得结果
解答 解:(1)用的是系统抽样.
(2)(0.040+0.060+0.050)×5=0.75
(3)众数是频率分布直方图中最高矩形的宽的中点横坐标,即$\frac{75+80}{2}$=77.5,
再根据中位数所在的垂直于横轴的直线平分所有矩形的面积,可得
中位数是75+$\frac{0.5+0.05+0.1-0.2}{0.060}$=77.5.
点评 本题主要考查系统抽样、中位数、众数的定义,频率分步直方图的应用,等可能事件的概率,属于基础题


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
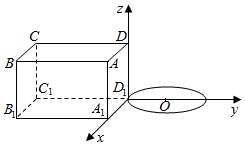 如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=2,DD1=1.
如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=2,DD1=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①④ | C. | ①②③ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最小值$\frac{1}{2}$,无最大值 | B. | 有最大值$\frac{1}{2}$,无最小值 | ||
| C. | 有最小值$\frac{1}{2}$,有最大值2 | D. | 无最大值,也无最小值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com