练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．函数$f（x）=x-\sqrt{1-2x}$（　　）
    A．有最小值$\frac{1}{2}$，无最大值B．有最大值$\frac{1}{2}$，无最小值
    C．有最小值$\frac{1}{2}$，有最大值2D．无最大值，也无最小值

    分析 先换元，再利用配方法，即可得出结论．

    解答 解：设$\sqrt{1-2x}$=t（t≥0），则y=$\frac{1-{t}^{2}}{2}$-t=-$\frac{1}{2}$（t+1）2+1，
    ∵t≥0，∴t=0函数有最大值$\frac{1}{2}$，无最小值．
    故选B．

    点评 本题考查函数的最值，考查换元配方法的运用，正确换元是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    2．一个三角形三边长分别为2cm、3cm、4cm，这个三角形最大角的余弦值是-$\frac{1}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

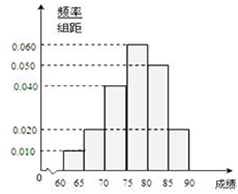    15．在某次综合素质测试中，共设有40个考室，每个考室30名考生．在考试结束后，为调查其测试前的培训辅导情况与测试成绩的相关性，抽取每个考室中座位号为05的考生，得到40名考生，统计他们的成绩，得到如图所示的频率分布直方图：
    （1）在这个调查采样中，用到的是什么抽样方法？
    （2）求分数在70～85之间的频率是多少？
    （3）求出这40名考生成绩的众数、中位数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．圆${（x+\frac{1}{2}）^2}+{（y+1）^2}=\frac{81}{16}$与圆${（x-sinθ）^2}+{（y-1）^2}=\frac{1}{16}（θ$为锐角）的位置关系是（　　）
    A．相离B．外切C．内切D．相交

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．若动直线x=a与函数f（x）=sinx和g（x）=2cos2x-1的图象分别交于M，N两点，则|MN|的最大值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知直线y=kx是曲线y=lnx的一条切线，则k的值为$\frac{1}{e}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的最小正周期为$\frac{2π}{3}$，最小值为-2，图象过（$\frac{5π}{9}$，0），求该函数的解析式并求其单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=xetx-ex+1，其中t∈R，e=2.71828…是自然对数的底数．
    （Ⅰ）当t=0时，求f（x）的最大值；
    （Ⅱ）若方程f（x）=1无实数根，求实数t的取值范围；
    （Ⅲ）若函数f（x）是（0，+∞）内的减函数，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{2\sqrt{5}}{5}$，直线x+2y+2=0与椭圆交于P，Q两点，且以PQ为直径的圆过M（2，0），求这个椭圆方程．

    查看答案和解析>>

    同步练习册答案