
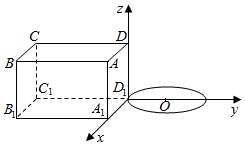
 如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=2,DD1=1.
如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=2,DD1=1.分析 (1)证明B1D1⊥A1C1,B1D1⊥CC1,即可证明B1D1⊥平面C1A1AC;
(2)(I)由题意sin∠OC1P=$\frac{1}{3}$,即可求C1N长度;
(Ⅱ)由(I)可知C1P=2$\sqrt{2}$,sin2∠OC1P=2×$\frac{1}{3}×\frac{2\sqrt{2}}{3}$=$\frac{4\sqrt{2}}{9}$,即可求$\overrightarrow{CQ}$•$\overrightarrow{CP}$的取值范围.
解答 (1)证明:在长方体ABCD-A1B1C1D1中,AB=BC,
∴B1D1⊥A1C1,B1D1⊥CC1,
∵A1C1∩CC1=C1,
∴B1D1⊥平面C1A1AC;
(2)(I)解:由题意sin∠OC1P=$\frac{1}{3}$,
∴cos∠OC1P=$\frac{2\sqrt{2}}{3}$,
∴C1N=$\frac{2}{\frac{2\sqrt{2}}{3}}$=$\frac{3}{2}\sqrt{2}$;
(Ⅱ)由(I)可知C1P=2$\sqrt{2}$,sin2∠OC1P=2×$\frac{1}{3}×\frac{2\sqrt{2}}{3}$=$\frac{4\sqrt{2}}{9}$,
∴cos2∠OC1P=$\frac{7}{9}$,
∴$\overrightarrow{CQ}$•$\overrightarrow{CP}$的最小值为$\frac{56}{9}$,最大值为8,
∴$\overrightarrow{CQ}$•$\overrightarrow{CP}$的取值范围是[$\frac{56}{9}$,8].
点评 本题考查线面垂直,考查平面向量知识的运用,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
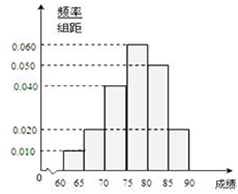 在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,得到40名考生,统计他们的成绩,得到如图所示的频率分布直方图:
在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,得到40名考生,统计他们的成绩,得到如图所示的频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在底面为菱形的四棱锥P-ABCD中,PA⊥平面ABCD,E为PD的中点,AB=2,∠ABC=$\frac{π}{3}$.
如图,在底面为菱形的四棱锥P-ABCD中,PA⊥平面ABCD,E为PD的中点,AB=2,∠ABC=$\frac{π}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com