练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若规定＝|ad－bc|，则不等式log<0的解集为________．


    　(0,1)∪(1,2)


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知等差数列{an}首项为a，公差为b，等比数列{bn}首项为b，公比为a，其中a、b都是大于1的正整数，且a1<b1，b2<a3，那么a＝________；若对于任意的n∈N*，总存在m∈N*，使得bn＝am＋3成立，则an＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若a>0且a≠1，b>0，则“logab>0”是“(a－1)(b－1)＞0”的(　　)

    A．充分不必要条件                                      B．必要不充分条件

    C．充要条件                                                 D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设偶函数f(x)满足f(x)＝2x－4(x≥0)，则{x|f(x－2)>0}＝(　　)

    A．{x|x<－2或x>4}                                      B．{x|x<0或x>4}

    C．{x|x<0或x>6}                                          D．{x|x<－2或x>2}

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设二次函数f(x)＝ax2＋bx＋c，函数F(x)＝f(x)－x的两个零点为m，n(m<n)．

    (1)若m＝－1，n＝2，求不等式F(x)>0的解集；

    (2)若a>0，且0<x<m<n<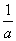，比较f(x)与m的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a≥0，b≥0，且a＋b＝2，则(　　)

    A．ab≤                                                    B．ab≥

    C．a2＋b2≥2                                                D．a2＋b2≤3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知直线x＋2y＝2分别与x轴、y轴相交于A，B两点，若动点P(a，b)在线段AB上，则ab的最大值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


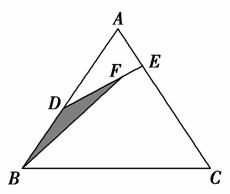
    如图所示，已知D是面积为1的△ABC的边AB的中点，E是边AC上任一点，连接DE，F是线段DE上一点，连接BF，设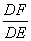＝λ1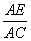，＝λ2，且λ1＋λ2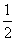＝，记△BDF的面积为S＝f(λ1，λ2)，则S的最大值是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


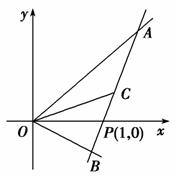
    如图，射线OA，OB分别与x轴正半轴成45°和30°角，过点P(1,0)作直线AB分别交OA，OB于A，B两点，当AB的中点C恰好落在直线y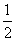＝x上时，求直线AB的方程．

     

    查看答案和解析>>

    同步练习册答案