练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．7个人排成一列，其中甲、乙两人相邻且与丙不相邻的方法种数是（　　）
    A．1200B．960C．720D．480

    分析 本题采用捆绑法和插空法进行排列，由分步计数原理可得结论．

    解答 解：将甲乙看作一个复合元素，和丙插入到剩下四人全排列所形成的5个空中的2个，
    故有A22A44A52=960，
    故选：B．

    点评 本题考查计数原理的运用，考查学生的计算能力，正确运用捆绑法和插空法是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    15．已知α是第三象限角，且sinα=-$\frac{3}{5}$．
    （Ⅰ）求tanα与tan（α-$\frac{π}{4}$）的值；
    （Ⅱ）求cos2α的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．设直线l与抛物线y2=4x相交于A，B两点，与圆（x-4）2+y2=r2（r＞0）相切于点M，且M为线段AB的中点，若这样的直线l恰有4条，则r的取值范围是（　　）
    A．（2，3）B．（2，4）C．$[2，2\sqrt{3}]$D．$（2，2\sqrt{3}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．把一颗骰子投掷两次，记第一次出现的点数为a，第二次出现的点数为b．已知方程组$\left\{\begin{array}{l}ax+by=2\\ 2x+y=3\end{array}\right.$．
    （Ⅰ）求方程组只有一个解的概率；
    （Ⅱ）若方程组每个解对应平面直角坐标系中点P（x，y），求点P落在第四象限的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=$\sqrt{{x}^{2}-ax+4}$在[1，+∞）上为增函数，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知（$\root{3}{x}$-$\frac{2}{x}$）n的展开式中，第三项的系数为144．
    （Ⅰ）求该展开式中所有偶数项的二项式系数之和；
    （Ⅱ）求该展开式的所有有理项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．若动直线x=a与函数f（x）=$\sqrt{3}$sin（x+$\frac{π}{6}$）和g（x）=sin（$\frac{π}{3}$-x）的图象分别交于M，N两点，则|MN|的最大值为（　　）
    A．1B．2C．$\sqrt{3}$D．1+$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

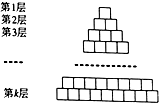    12．如图，由若干个小正方形组成的k层三角形图阵，第一层有1个小正方形，第二层有2个小正方形，依此类推，第k层有k个小正方形，除去最底下的一层，每个小正方形都放置在它下一层的两个小正方形之上．现对第k层的每个小正方形用数字进行标注，从左到右依次记为x1，x2，…xk，其中xi∈{0，1}（1≤i≤k），其它小正方形标注的数字是它下面两个小正方形标注的数字之和，依此规律，记第一层的小正方形标注的数字为x0；
    （1）当k=4时，若要求x0为2的倍数，则有多少种不同的标注方法？
    （2）当k=11时，若要求x0为3的倍数，则有多少种不同的标注方法？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．在△ABC中，角A、B、C所对的边分别是a、b、c，且满足csinA-$\sqrt{3}$acosC=0．
    （1）求角C的大小；
    （2）若c=2，求△ABC的面积S的最大值．

    查看答案和解析>>

    同步练习册答案