
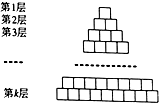
 如图,由若干个小正方形组成的k层三角形图阵,第一层有1个小正方形,第二层有2个小正方形,依此类推,第k层有k个小正方形,除去最底下的一层,每个小正方形都放置在它下一层的两个小正方形之上.现对第k层的每个小正方形用数字进行标注,从左到右依次记为x1,x2,…xk,其中xi∈{0,1}(1≤i≤k),其它小正方形标注的数字是它下面两个小正方形标注的数字之和,依此规律,记第一层的小正方形标注的数字为x0;
如图,由若干个小正方形组成的k层三角形图阵,第一层有1个小正方形,第二层有2个小正方形,依此类推,第k层有k个小正方形,除去最底下的一层,每个小正方形都放置在它下一层的两个小正方形之上.现对第k层的每个小正方形用数字进行标注,从左到右依次记为x1,x2,…xk,其中xi∈{0,1}(1≤i≤k),其它小正方形标注的数字是它下面两个小正方形标注的数字之和,依此规律,记第一层的小正方形标注的数字为x0;分析 (1)确定x0=x1+3x2+3x3+x4.因为x0为2的倍数,所以x1+x2+x3+x4是2的倍数,则x1,x2,x3,x4四个都取0或两个取0两个取1或四个都取1,即可得到标注方法;
(2)确定只要x1+C101x2+C109x10+x11是3的倍数,即只要x1+x2+x10+x11是3的倍数,所以x1、x2、x10、x11四个都取0或三个取1一个取0,而其余七个可以取0或1,即可得到标注方法.
解答 解:(1)当k=4时,第4层标注数字依次为x1,x2,x3,x4,第3层标注数字依次为x1+x2,x2+x3,x3+x4,第2层标注数字依次为x1+2x2+x3,x2+2x3+x4,所以x0=x1+3x2+3x3+x4.
因为x0为2的倍数,所以x1+x2+x3+x4是2的倍数,则x1,x2,x3,x4四个都取0或两个取0两个取1或四个都取1,所以共有1+C42+1=8种标注方法.
(2)当k=11时,第11层标注数字依次为x1,x2,…,x11,第10层标注数字依次为x1+x2,x2+x3,…,x10+x11,第9层标注数字依次为x1+2x2+x3,x2+2x3+x4,…,x9+2x10+x11,以此类推,可得x0=x1+C101x2+…+C109x10+x11.
因为C102=C108=45,C103=C107=120,C104=C106=210,C105=252均为3的倍数,所以只要x1+C101x2+C109x10+x11是3的倍数,即只要x1+x2+x10+x11是3的倍数,
所以x1、x2、x10、x11四个都取0或三个取1一个取0,而其余七个可以取0或1,这样共有(1+C43)×27=640种标注方法.
点评 本题考查进行简单的合情推理,考查学生分析解决问题的能力,有难度.


科目:高中数学 来源: 题型:选择题
| A. | y=2sin($\frac{1}{2}$x+$\frac{π}{6}$) | B. | y=$\frac{1}{2}$sin(2x-$\frac{π}{6}$) | C. | y=2sin($\frac{1}{2}$x-$\frac{π}{6}$) | D. | y=$\frac{1}{2}$sin(2x+$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com