
分析 (Ⅰ)求出原函数的导函数,得到f'(4)=e2,又f(4)=e2,则函数f(x)在点(4,f(4))的切线方程为y-e2=e2(x-4),即y=e2x-3e2;
(Ⅱ)求出原函数的导函数,根据a的取值对函数的单调性加以判断,当a=1时,g(x)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增,对任意x∈(0,+∞),不等式g(x)≥g(1)=0恒成立,符合题意,即a=1,从而求出实数a的取值的集合M;
(Ⅲ)把a的值代入函数解析式,然后求函数的导函数,求出导函数的零点,由导函数的零点把定义域分段,根据导函数在各区间段内的符号求出原函数的单调区间.
解答 解:(Ⅰ)∵$f'(x)=\frac{e^x}{e^2}$,∴f'(4)=e2,又∵f(4)=e2,
∴函数f(x)在点(4,f(4))的切线方程为y-e2=e2(x-4),
即y=e2x-3e2; …(3分)
(Ⅱ)由g(1)=0及题设可知,对任意x∈(0,+∞),不等式g(x)≥g(1)恒成立,
∴函数g(x)=xlnx-a(x-1)必在x=1处取得极小值,即g'(1)=0,…(4分)
∵g'(x)=lnx+1-a,∴g'(1)=1-a=0,即a=1,…(5分)
当a=1时,g'(x)=lnx,∴x∈(0,1),g'(x)<0;x∈(1,+∞),g'(x)>0,
∴g(x)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增,
则g(x)min=g(1)=0…(6分)
∴对任意x∈(0,+∞),不等式g(x)≥g(1)=0恒成立,符合题意,即a=1,
∴M={1}; …(7分)
(Ⅲ)由(Ⅱ)a=1,
∴函数$h(x)=f(x)-g(x)=\frac{e^x}{e^2}-xlnx+x-1$,其定义域为(0,+∞),
求得$h'(x)=(\frac{e^x}{e^2}-xlnx+x-1)'=\frac{e^x}{e^2}-lnx$,…(8分)
令m(x)=h'(x),$m'(x)=\frac{e^x}{e^2}-\frac{1}{x}$为区间(0,+∞)上的增函数,…(9分)
设x0为函数m'(x)的零点,即$\frac{{{e^{x_0}}}}{e^2}=\frac{1}{x_0}$,则${x_0}=\frac{e^2}{{{e^{x_0}}}}$,
∵当0<x<x0时,m'(x)<0;当x>x0时,m'(x)>0,
∴函数m(x)=h'(x)在区间(0,x0)上为减函数,在区间(x0,+∞)上为增函数,
∴$h'(x)≥h'({x_0})=\frac{{{e^{x_0}}}}{e^2}-ln{x_0}=\frac{1}{x_0}-ln\frac{e^2}{{{e^{x_0}}}}=\frac{1}{x_0}+{x_0}-2≥0$,
∴函数h(x)在区间(0,+∞)上为增函数. …(12分)
点评 本题主要考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.考查了利用导数研究含有参数的不等式恒成立问题,是难题.


科目:高中数学 来源: 题型:选择题
| A. | (2,3) | B. | (2,4) | C. | $[2,2\sqrt{3}]$ | D. | $(2,2\sqrt{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
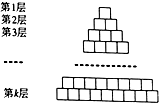 如图,由若干个小正方形组成的k层三角形图阵,第一层有1个小正方形,第二层有2个小正方形,依此类推,第k层有k个小正方形,除去最底下的一层,每个小正方形都放置在它下一层的两个小正方形之上.现对第k层的每个小正方形用数字进行标注,从左到右依次记为x1,x2,…xk,其中xi∈{0,1}(1≤i≤k),其它小正方形标注的数字是它下面两个小正方形标注的数字之和,依此规律,记第一层的小正方形标注的数字为x0;
如图,由若干个小正方形组成的k层三角形图阵,第一层有1个小正方形,第二层有2个小正方形,依此类推,第k层有k个小正方形,除去最底下的一层,每个小正方形都放置在它下一层的两个小正方形之上.现对第k层的每个小正方形用数字进行标注,从左到右依次记为x1,x2,…xk,其中xi∈{0,1}(1≤i≤k),其它小正方形标注的数字是它下面两个小正方形标注的数字之和,依此规律,记第一层的小正方形标注的数字为x0;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 观察下列各个等式:12=1,12+22=5,12+22+32=14,12+22+32+42=30,….
观察下列各个等式:12=1,12+22=5,12+22+32=14,12+22+32+42=30,….查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最大值-$\frac{3}{2}-$ln2,无最小值 | B. | 有最小值-$\frac{3}{2}$-ln2,无最大值 | ||
| C. | 无最大值也无最小值 | D. | 有最大值4ln2,且有最小值-$\frac{3}{2}$-ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com