
分析 (Ⅰ)利用诱导公式化简即可得解.
(Ⅱ)首先利用弦切互化公式及正弦的倍角公式对原式进行变形,再两次运用和差化积公式,同时结合正余弦互化公式,则问题解决.
解答 (本题满分为12分)
解:(Ⅰ)$\frac{\sqrt{1-2sin100°cos280°}}{cos370°-\sqrt{1-co{s}^{2}170°}}$=$\frac{\sqrt{1-2sin80°cos80°}}{cos10°-sin10°}$=$\frac{sin80°-cos80°}{cos10°-sin10°}$=$\frac{cos10°-sin10°}{cos10°-sin10°}$=1;…6分
(Ⅱ)tan20°+4sin20°
=$\frac{sin20°+4sin20°cos20°}{cos20°}$
=$\frac{sin20°+2sin40°}{cos20°}$
=$\frac{(sin20°+sin40°)+sin40°}{cos20°}$
=$\frac{2sin30°cos10°+sin40°}{cos20°}$
=$\frac{sin80°+sin40°}{cos20°}$
=$\frac{2sin60°cos20°}{cos20°}$
=$\sqrt{3}$.…12分
点评 本题主要考查了三角函数式的恒等变形及运算能力,考查了转化思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$| | B. | ($\overrightarrow{a}$•$\overrightarrow{b}$)2=$\overrightarrow{{a}^{2}}$•$\overrightarrow{{b}^{2}}$ | C. | 若$\overrightarrow{a}$⊥($\overrightarrow{b}$-$\overrightarrow{c}$)则$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$ | D. | 若$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$则$\overrightarrow{b}$=$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
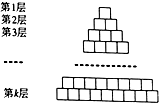 如图,由若干个小正方形组成的k层三角形图阵,第一层有1个小正方形,第二层有2个小正方形,依此类推,第k层有k个小正方形,除去最底下的一层,每个小正方形都放置在它下一层的两个小正方形之上.现对第k层的每个小正方形用数字进行标注,从左到右依次记为x1,x2,…xk,其中xi∈{0,1}(1≤i≤k),其它小正方形标注的数字是它下面两个小正方形标注的数字之和,依此规律,记第一层的小正方形标注的数字为x0;
如图,由若干个小正方形组成的k层三角形图阵,第一层有1个小正方形,第二层有2个小正方形,依此类推,第k层有k个小正方形,除去最底下的一层,每个小正方形都放置在它下一层的两个小正方形之上.现对第k层的每个小正方形用数字进行标注,从左到右依次记为x1,x2,…xk,其中xi∈{0,1}(1≤i≤k),其它小正方形标注的数字是它下面两个小正方形标注的数字之和,依此规律,记第一层的小正方形标注的数字为x0;查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 2 | C. | -2 | D. | -8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com