
分析 方法一:g(x)=f(x)-ax在区间(0,4)上有三个零点可化为|lnx|-ax=0在区间(0,4)上有三个不同的解,令令a=$\frac{|lnx|}{x}$=$\left\{\begin{array}{l}{-\frac{lnx}{x},0<x<1}\\{\frac{lnx}{x},1≤x<4}\end{array}\right.$;讨论函数的取值即可,
方法二:首先,画出函数y=|lnx|的图象,然后,借助于图象,结合在区间(0,4)上有三个零点,进行判断
解答 解:方法一:∵g(x)=f(x)-ax在区间(0,4)上有三个零点,
∴|lnx|-ax=0在区间(0,4)上有三个不同的解,
令a=$\frac{|lnx|}{x}$=$\left\{\begin{array}{l}{-\frac{lnx}{x},0<x<1}\\{\frac{lnx}{x},1≤x<4}\end{array}\right.$;
则当0<x<1时,-$\frac{lnx}{x}$的值域为(0,+∞);
当1≤x<4时,a=$\frac{lnx}{x}$在[1,e]上是增函数,
0≤$\frac{lnx}{x}$≤$\frac{1}{e}$,
在[e,4)上是减函数,
$\frac{ln2}{2}$≤$\frac{lnx}{x}$≤$\frac{1}{e}$;
故当a∈($\frac{ln2}{2}$,$\frac{1}{e}$)时,有三个不同的解.
方法二:函数y=|lnx|的图象如图示
当a≤0时,显然,不合乎题意,
当a>0时,如图示
当x∈(0,1]时,存在一个零点,
当x>1时,f(x)=lnx,
可得g(x)=lnx-ax,(x∈(1,3])
g′(x)=$\frac{1}{x}$-a=$\frac{1-ax}{x}$,
若g′(x)<0,可得x>$\frac{1}{a}$,g(x)为减函数,
若g′(x)>0,可得x<$\frac{1}{a}$,g(x)为增函数,
此时f(x)必须在(1,4)上有两个交点,
∴$\left\{\begin{array}{l}{g(\frac{1}{a})>0}\\{g(4)<0}\\{g(1)≤0}\end{array}\right.$,
解得,$\frac{ln2}{2}$≤a<$\frac{1}{e}$,
在区间(0,3]上有三个零点时,
故实数a的取值范围为($\frac{ln2}{2}$,$\frac{1}{e}$),
故答案为:($\frac{ln2}{2}$,$\frac{1}{e}$).
点评 本题考查了函数的零点与方程的根及函数的取值的关系应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
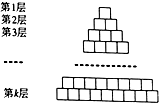 如图,由若干个小正方形组成的k层三角形图阵,第一层有1个小正方形,第二层有2个小正方形,依此类推,第k层有k个小正方形,除去最底下的一层,每个小正方形都放置在它下一层的两个小正方形之上.现对第k层的每个小正方形用数字进行标注,从左到右依次记为x1,x2,…xk,其中xi∈{0,1}(1≤i≤k),其它小正方形标注的数字是它下面两个小正方形标注的数字之和,依此规律,记第一层的小正方形标注的数字为x0;
如图,由若干个小正方形组成的k层三角形图阵,第一层有1个小正方形,第二层有2个小正方形,依此类推,第k层有k个小正方形,除去最底下的一层,每个小正方形都放置在它下一层的两个小正方形之上.现对第k层的每个小正方形用数字进行标注,从左到右依次记为x1,x2,…xk,其中xi∈{0,1}(1≤i≤k),其它小正方形标注的数字是它下面两个小正方形标注的数字之和,依此规律,记第一层的小正方形标注的数字为x0;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 观察下列各个等式:12=1,12+22=5,12+22+32=14,12+22+32+42=30,….
观察下列各个等式:12=1,12+22=5,12+22+32=14,12+22+32+42=30,….查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最大值-$\frac{3}{2}-$ln2,无最小值 | B. | 有最小值-$\frac{3}{2}$-ln2,无最大值 | ||
| C. | 无最大值也无最小值 | D. | 有最大值4ln2,且有最小值-$\frac{3}{2}$-ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②③ | C. | ①③ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com