
分析 由等差数列的通项公式求出数列{$\frac{1}{{a}_{n}}$}的通项公式,证明数列{S2n+1-Sn}(n∈N*)是递减数列,可求其最大值,进而可得m的取值范围,结合m为正整数可得.
解答 解:等差数列{an}中,a1=1,a6=21=a1+5d,∴公差 d=4,an=1+(n-1)d=4n-3,$\frac{1}{{a}_{n}}$=$\frac{1}{4n-3}$.
记数列$\{\frac{1}{a_n}\}$的前n项和为Sn,则Sn =$\frac{1}{1}$+$\frac{1}{5}$+$\frac{1}{9}$+…+$\frac{1}{4n-3}$,
∵(S2n+1-Sn)-(S2n+3-Sn+1)=($\frac{1}{{a}_{n+1}}$+$\frac{1}{{a}_{n+2}}$+…+$\frac{1}{{a}_{2n+1}}$)-($\frac{1}{{a}_{n+2}}$+$\frac{1}{{a}_{n+3}}$+…+$\frac{1}{{a}_{2n+3}}$)
=$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{2n+2}}$-$\frac{1}{{a}_{2n+3}}$=$\frac{1}{4n+1}$-$\frac{1}{8n+5}$-$\frac{1}{8n+9}$=($\frac{1}{8n+2}$-$\frac{1}{8n+5}$)+($\frac{1}{8n+2}$-$\frac{1}{8n+9}$)>0,
∴数列{S2n+1-Sn}(n∈N*)是递减数列,
∴数列{S2n+1-Sn}(n∈N*)的最大项为S3-S1=$\frac{1}{5}$+$\frac{1}{9}$=$\frac{14}{45}$,
∴由题意可得,只需$\frac{14}{45}$≤$\frac{m}{15}$,即 m≥$\frac{14}{3}$,又∵m是正整数,∴m的最小值为5,
故答案为:5.
点评 本题考查数列与不等式的结合,证数列{S2n+1-Sn}(n∈N*)是递减数列并求数列{S2n+1-Sn}(n∈N*)的最大值是解决问题的关键,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-2018,-2016) | B. | (-∞,-2018) | C. | (-2016,-2015) | D. | (-∞,-2012) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
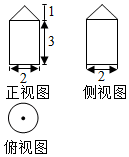
| A. | $\frac{10}{3}π$ | B. | 3π | C. | 4π | D. | $(6+\sqrt{2}π)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com