练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．下列各选项中的对象能构成集合的是（　　）
    A．好教师B．未来世界的高科技产品
    C．2014年巴西世界杯的参赛国D．上海世博会好看的展馆

    分析 分别利用集合的确定性，互异性确定各选项是否构成集合．

    解答 解：A，由于好教师的标准不确定，所以元素无法确定，所以不能构成集合；
    B，因为未来世界的高科技产品是不确定的，所以不能构成集合；
    C，2014年巴西世界杯的参赛国是确定的、互异的，所以能构成集合；
    D，由于上海世博会好看的展馆标准不确定，所以元素无法确定，所以不能构成集合；
    故选：C．

    点评 本题主要考查集合元素的性质，利用集合的确定性和互异性是判断集合的一种方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    13．把一颗骰子投掷两次，记第一次出现的点数为a，第二次出现的点数为b．已知方程组$\left\{\begin{array}{l}ax+by=2\\ 2x+y=3\end{array}\right.$．
    （Ⅰ）求方程组只有一个解的概率；
    （Ⅱ）若方程组每个解对应平面直角坐标系中点P（x，y），求点P落在第四象限的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

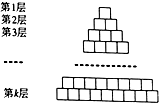    12．如图，由若干个小正方形组成的k层三角形图阵，第一层有1个小正方形，第二层有2个小正方形，依此类推，第k层有k个小正方形，除去最底下的一层，每个小正方形都放置在它下一层的两个小正方形之上．现对第k层的每个小正方形用数字进行标注，从左到右依次记为x1，x2，…xk，其中xi∈{0，1}（1≤i≤k），其它小正方形标注的数字是它下面两个小正方形标注的数字之和，依此规律，记第一层的小正方形标注的数字为x0；
    （1）当k=4时，若要求x0为2的倍数，则有多少种不同的标注方法？
    （2）当k=11时，若要求x0为3的倍数，则有多少种不同的标注方法？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．定义“等和数列”：在一个数列，如果每一项与它的后一项的和都为同一个常数，那么这个数列叫做等和数列，这个常数叫做该数列的公和．已知数列{an}是等和数列，且a1=2，公和为5，则a18的值为3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．若函数f（x）=x2-2x+alnx存在两个极值点x1，x2（x1＜x2），则t＜$\frac{f（{x}_{1}）}{{x}_{2}}$恒成立，则t（　　）
    A．有最大值-$\frac{3}{2}-$ln2，无最小值B．有最小值-$\frac{3}{2}$-ln2，无最大值
    C．无最大值也无最小值D．有最大值4ln2，且有最小值-$\frac{3}{2}$-ln2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知数列{an}的首项a1=4，前n项和为Sn，且Sn+1-3Sn-2n-4=0（n∈N+）
    （1）证明数列{an+1}为等比数列，并求数列{an}的通项公式；
    （2）设函数f（x）=anx+an-1x2+…+a1xn，f′（x）是函数f（x）的导函数，求f′（1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．在△ABC中，角A、B、C所对的边分别是a、b、c，且满足csinA-$\sqrt{3}$acosC=0．
    （1）求角C的大小；
    （2）若c=2，求△ABC的面积S的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知向量$\overrightarrow a$=（1，2），$\overrightarrow b$=（x，4），若$\overrightarrow a$∥$\overrightarrow b$，则实数x的值为（　　）
    A．8B．2C．-2D．-8

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．如图，在半径为$\sqrt{3}$，圆心角为60°的扇形的弧上任取一点P，作扇形的内接矩形PNMQ，使点Q在OA上，点N，M在OB上，设矩形PNMQ的面积为y，∠POB=θ．
    （Ⅰ）将y表示成θ的函数关系式，并写出定义域；
    （Ⅱ）求矩形PNMQ的面积取得最大值时$\overrightarrow{OP}$•$\overrightarrow{ON}$的值；
    （Ⅲ）求矩形PNMQ的面积y≥$\frac{\sqrt{6}-\sqrt{3}}{2}$的概率．

    查看答案和解析>>

    同步练习册答案