练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知双曲线-=1(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为(　　)

    (A)2 (B)2 (C)4 (D)4


    B

    解析:双曲线左顶点为A1(-a,0),

    渐近线为y=±x,

    抛物线y2=2px(p>0)焦点为F（,0）,

    准线为直线x=-.

    由题意知-=-2,

    ∴p=4,

    由题意知2+a=4,

    ∴a=2.

    ∴双曲线渐近线y=±x中与准线x=-交于(-2,-1)的渐近线为y=x,

    ∴-1=×(-2),

    ∴b=1.

    ∴c2=a2+b2=5,

    ∴c=,

    ∴2c=2.故选B.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在平面直角坐标系xOy中,若双曲线-=1的离心率为,则m的值为　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知椭圆+=1的两个焦点是F1、F2,点P在该椭圆上,若|PF1|-|PF2|=2,则△PF1F2的面积是　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示,中心均为原点O的双曲线与椭圆有公共焦点,M、N是双曲线的两顶点.若M,O,N将椭圆长轴四等分,则双曲线与椭圆的离心率的比值是(　　)

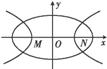
     (A)3   (B)2           (C)   (D)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知椭圆C1: +=1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.

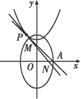
    (1)求椭圆C1的方程;

    (2)设点P在抛物线C2:y=x2+h(h∈R)上,C2在点P处的切线与C1交于点M,N.当线段AP的中点与MN的中点的横坐标相等时,求h的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,抛物线E:y2=4x的焦点为F,准线l与x轴的交点为A.点C在抛物线E上,以C为圆心,|CO|为半径作圆,设圆C与准线l交于不同的两点M,N.

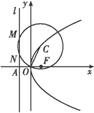
     (1)若点C的纵坐标为2,求|MN|;

    (2)若|AF|2=|AM|·|AN|,求圆C的半径.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    过椭圆+=1(a>b>0)的焦点垂直于x轴的弦长为,则双曲线-=1的离心率e的值是(　　)

    (A)   (B)

    (C)   (D)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某校要从高一、高二、高三共2 012名学生中选取50名组成志愿团，若采用下面的方法选取，先用简单随机抽样的方法从2 012人中剔除12人，剩下的2 000人再按分层抽样的方法进行，则每人入选的概率(　　)

    A．都相等且为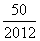                     B．都相等且为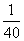

    C．不会相等                             D．均不相等

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    现采用随机模拟的方法估计该运动员射击4次，至少击中3次的概率：先由计算器给出0到9之间取整数值的随机数，指定0、1表示没有击中目标，2、3、4、5、6、7、8、9表示击中目标，以4个随机数为一组，代表射击4次的结果，经随机模拟产生了 20组随机数：

    7 527　0 293　 7 140　9 857　0 347　4 373　8 636　6 947

    1 417　4 698   0 371　6 233　2 616　8 045　6 011　3 661

    9 597　7 424　 7 610　4 281

    根据以上数据估计该射击运动员射击4次至少击中3次的概率为 (　　)

    A．0.852  B．0.819 2  C．0.8  D．0.75

    查看答案和解析>>

    同步练习册答案