
| A. | (-∞,-$\frac{3}{4}$)∪(0,$\frac{3}{4}$) | B. | (-∞,0)∪(0,$\frac{3}{4}$) | C. | (-∞,-1)∪(0,1) | D. | (-∞,0)∪(0,1) |
分析 取特殊点P(0,2),P(0,-2),求出$\frac{{k}_{PB}}{{k}_{QF}}$,利用排除法,可得结论.
解答 解:取特殊点P(0,2),则PA方程为y=x+2
与椭圆方程联立,可得7x2+16x+4=0=0,所以x=-2或-$\frac{2}{7}$,所以Q(-$\frac{2}{7}$,$\frac{12}{7}$),
∴kPB=-1,kQF=$\frac{\frac{12}{7}}{-\frac{2}{7}-1}$=-$\frac{3}{4}$,
∴$\frac{{k}_{PB}}{{k}_{QF}}$=$\frac{3}{4}$.
同理取P(0,-2),$\frac{{k}_{PB}}{{k}_{QF}}$=-$\frac{3}{4}$.
根据选项,排除A,B,C,
故选D.
点评 本题考查圆与圆锥曲线的综合,考查特殊法的运用,属于中档题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:解答题
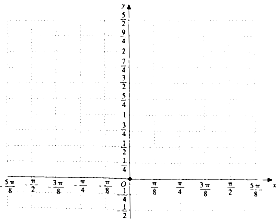 已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$.
已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
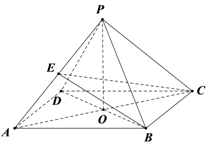 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,AC∩BD=O
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,AC∩BD=O查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3} | B. | {5,6} | C. | {4,5,6} | D. | {4,5,6,7} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<$\frac{3}{2}$} | B. | {x|x>$\frac{3}{2}$或x<-1} | C. | {x|-$\frac{3}{2}$<x<1} | D. | {x|x>1或x<-$\frac{3}{2}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1009 | B. | -1008 | C. | -1007 | D. | -1006 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com