
分析 (1)利用线面平行的判定证明;
(2)过A作AH⊥A1E与H,JAH交A1E于G,则AH⊥面A1EFD1,
线段AG的长是直线AD到平面A1EFD1的距离,△AA1H∽△AGA1,则有$\frac{AG}{A{A}_{1}}=\frac{A{A}_{1}}{AH}$⇒AG即可.
解答 解:(1)证明:如图,∵E,F分别是BB1,CC1的中点,∴EF∥A1D1,∴四点A1、E、F、D1共面.
∵AD∥EF,AD?面A1EFD1,EF?A1EFD1∴AD∥平面A1EFD1
(2)正方体ABCD-A1B1C1D1中面 AA1B1B中⊥面A1EFD1.
过A作AH⊥A1E与H,JAH交A1E于G,则AH⊥面A1EFD1,
线段AG的长是直线AD到平面A1EFD1的距离,
△AA1H∽△AGA1,则有$\frac{AG}{A{A}_{1}}=\frac{A{A}_{1}}{AH}$⇒AG=$\frac{2\sqrt{5}}{5}a$
∴直线AD到平面A1EFD1的距离为$\frac{{2\sqrt{5}}}{5}a$.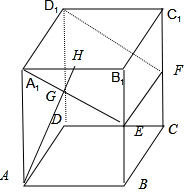
点评 本题考查了空间线面平行的判定,线面距离,属于中档题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (0,1) | C. | (1,+∞) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
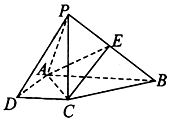 如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,AB=2AD=2CD=4,PC=2a,E是PB的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,AB=2AD=2CD=4,PC=2a,E是PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2$\sqrt{3}$-2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 2 | 3 | 4 |
| y | 2 | 4.2 | 4.5 | 4.6 | m |
| A. | 5.6 | B. | 5.3 | C. | 5.0 | D. | 4.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |a+b|≥a-b | B. | $2\sqrt{ab}≤|{a+b}|$ | C. | |a+b|<|a|+|b| | D. | $|{\frac{b}{a}+\frac{a}{b}}|≥2$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com