设全集U=R，A={x|x(x-2)<0}，B={x|y=ln(1-x)<0}，则图中阴影部分表示的集合为( )
A．{x|0<x≤1} B．{x|1≤x<2}
C．{x|x≥1} D．{x|x≤1}
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目：高中数学 来源：2013-2014学年湖南省益阳市高三模拟考试文科数学试卷（解析版） 题型：选择题
已知双曲线
的一个焦点与抛物线
的焦点重合，且双曲线的离心率等于
，则该双曲线的方程为（ ）
A．
B．
C．
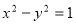D．
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖南省怀化市高三第二次模拟考试文科数学试卷（解析版） 题型：选择题
一个算法的程序框图如图所示，其输出结果是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省黄冈市高三5月适应性考试理科数学试卷（解析版） 题型：填空题
1955年，印度数学家卡普耶卡（D.R.Kaprekar）研究了对四位自然数的一种交换：任给出四位数
，用的四个数字由大到小重新排列成一个四位数m，再减去它的反序数n(即将的四个数字由小到大排列，规定反序后若左边数字有0，则将0去掉运算，比如0001，计算时按1计算)，得出数
，然后继续对
重复上述变换，得数
，…，如此进行下去，卡普耶卡发现，无论是多大的四位数，只要四个数字不全相同，最多进行k次上述变换，就会出现变换前后相同的四位数t(这个数称为Kaprekar变换的核).通过研究10进制四位数2014可得Kaprekar变换的核为 .
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省黄冈市高三5月适应性考试理科数学试卷（解析版） 题型：选择题
甲乙两人从4门课程中各选修两门，则甲乙所选的课程中至少有1门不相同的选法共有( )种
A.30 B.36 C.60 D.72
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省黄冈市高三5月适应性考试文科数学试卷（解析版） 题型：解答题
已知数列
的首项
，且对任意
都有
（其中
为常数）.
（1）若数列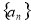
为等差数列，且
，求
的通项公式.
（2）若数列是等比数列，且
，从数列中任意取出相邻的三项，均能按某种顺序排成等差数列，求的前
项和
成立的
的取值的集合.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省黄冈市高三5月适应性考试文科数学试卷（解析版） 题型：填空题
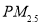是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，如图是根据某地某日早7点至晚8点甲、乙两个监测点统计的数据（单位：毫克/每立方米）列出的茎叶图，则甲、乙两地浓度的方差较小的是 。
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省黄冈市高三第二学期三月月考理科数学试卷（解析版） 题型：填空题
设
为不小于2的正整数，对任意
，若
（其中
，
，且
），则记
，如
，
.下列关于该映射
的命题中，正确的是.
①若
，
，则
②若，
，
，且
，则
③若，，
，
，且，
，则
④若，，，，且，，则
.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省黄冈市高三下学期三月月考理科数学试卷（解析版） 题型：解答题
已知等比数列
的各项均为正数，且
成等差数列，
成等比数列.
（1）求数列的通项公式；
（2）已知
，记
，
,求证：
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
，所以图中阴影部分表示的集合为
.
