已知函数f(x)=x3-3ax2+3bx
(1)若a=1,b=0,求f'(2)的值;
(2)若f(x)的图象与直线12x+y-1=0相切于点(1,-11),求a,b的值;
(3)在(2)的条件下,求函数f(x)的单调区间.
解:(1)求导数得f'(x)=3x
2-6ax+3b,…(3分)
当a=1,b=0时,f'(x)=3x
2-6x=3x(x-2),
∴f'(2)=0…(4分)
(2)由于f(x)的图象与直线12x+y-1=0相切于点(1,-11),
所以
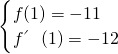
…(6分)
即
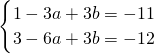
,解得a=1,b=-3…(9分)
(3)由a=1,b=-3得:f'(x)=3x
2-6ax+3b=3(x
2-2x-3)=3(x+1)(x-3)…(10分)
由f'(x)>0,解得x<-1或x>3;由f'(x)<0,解得-1<x<3.--------------------(13分)
故函数f(x)在区间(-∞,-1),(3,+∞)上单调递增,在区间(-1,3)上单调递减.---(14分)
分析:(1)求导数,代入相应的值,可得f'(2)的值;
(2)利用f(x)的图象与直线12x+y-1=0相切于点(1,-11),建立方程组,即可求a,b的值;
(3)利用导数的正负,即可求得函数f(x)的单调区间.
点评:本小题主要考查导数、函数解析式、函数极值、函数的单调性、单调区间等知识,考查待定系数、化归与转化数学思想方法,综合运用能力和运算求解能力.

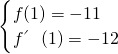 …(6分)
…(6分)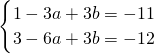 ,解得a=1,b=-3…(9分)
,解得a=1,b=-3…(9分)

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<