
图1-19
科目:高中数学 来源: 题型:044
(2007
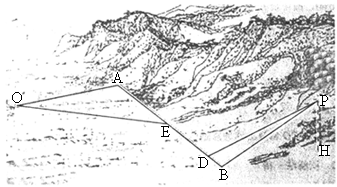
湖南,19)如图所示,某地为了开发旅游资源,欲修建一条连接风景点P和居民区O的公路.点P所在的山坡面与山脚所在水平面α所成的二面角为θ(0°<θ<90°),且 ,点P到平面α的距离PH=0.4(km).沿山脚原有一段笔直的公路AB可供利用.从点O到山脚修路的造价为a万元/km,原有公路改建费用为
,点P到平面α的距离PH=0.4(km).沿山脚原有一段笔直的公路AB可供利用.从点O到山脚修路的造价为a万元/km,原有公路改建费用为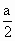 万元/km.当山坡上公路长度为lkm(1≤l≤2)时,其造价为
万元/km.当山坡上公路长度为lkm(1≤l≤2)时,其造价为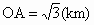 .
.
(1)
在AB上求一点D,使沿折线PDAO修建公路的总造价最小:(2)
对于(1)中得到的点D,在DA上求一点E,使沿折线PDEO修建公路的总造价最小;(3)
在AB上是否存在两个不同的点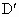 、
、 ,使沿折线
,使沿折线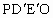 修建公路的总造价小于(2)中得到的最小总造价,证明你的结论.
修建公路的总造价小于(2)中得到的最小总造价,证明你的结论.查看答案和解析>>
科目:高中数学 来源: 题型:
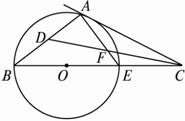
图2-4-19
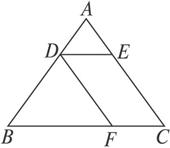
(1)求∠ADF的度数.
(2)若∠ACB的度数为y度,∠B的度数为x度,那么y与x之间有怎样的关系?试写出你的猜测并给出证明.
(3)若AB =AC,求AC∶BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
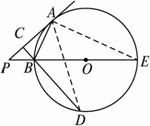
图2-5-19
(1)求证:AB2=PB·BD.
(2)若PA =15,PB =5,求BD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)在AB上求一点D,使沿折线PDAO修建公路的总造价最小;
(2)对于(1)中得到的点D,在DA上求一点E,使沿折线PDEO修建公路的总造价最小;
(3)在AB上是否存在两个不同的点D′,E′,使沿折线.PD′E′O修建公路的总造价小于(2)中得到的最小总造价?证明你的结论.

a)
第19题图
(文)如图b所示,直四棱柱ABCD-A1B1C1D1中,∠ADC=90°,△ABC为等边三角形,且AA1=AD=DC=2.
(1)求AC1与BC所成角的余弦值;
(2)求二面角C1-BD-C的大小;
(3)设M是BD上的点,当DM为何值时,D1M⊥平面A1C1D?并证明你的结论.

第19题图
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求证:AC⊥平面BB1C1C;
(2)当α为何值时,AB1⊥BC1,且使D点恰为BC的中点?并说明理由;
(3)当AB1⊥BC1,且D为BC中点时,若BC=2,四棱锥A-BB1C1C的体积为![]() ,求二面角A-B1C1-C的大小.
,求二面角A-B1C1-C的大小.
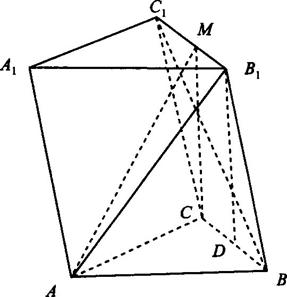
第19题图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com