
已知函数f(x)=alnx+x2(a为实常数).
(1)若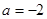 ,求证:函数f(x)在(1,+∞)上是增函数;
,求证:函数f(x)在(1,+∞)上是增函数;
(2)当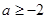 时,求函数f(x)在[1,e]上的最小值及相应的x值;
时,求函数f(x)在[1,e]上的最小值及相应的x值;
(3)若存在x∈[1,e],使得f(x)≤(a+2)x成立,求实数a的取值范围
(1)见解析;(2)当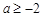 时,
时,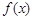 的最小值为1,相应的x值为1;(3)
的最小值为1,相应的x值为1;(3)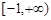 .
.
【解析】(1)直接对f(x)求导,说明当x>1时,导数大于零即可.
(2)利用导数求极值最值,最值不在区间端点出取得,就在极值处取得,因而比较极值及端点值即可确定最值.
(3)由于x>0,所以此不等式可转化为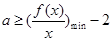 .然后构造函数
.然后构造函数 求它的最小值即可,要注意恒成立问题与存在性问题的区别.
求它的最小值即可,要注意恒成立问题与存在性问题的区别.
解:(1)当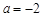 时,
时,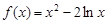 ,当
,当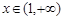 ,
,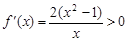 ,
,
故函数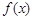 在
在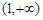 上是增函数;------------(3分)
上是增函数;------------(3分)
(2)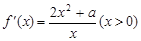 ,当
,当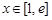 ,
,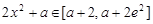 ,
,
当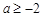 时,
时,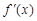 在
在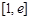 上非负(仅当
上非负(仅当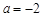 ,x=1时,
,x=1时, ),
),
故函数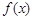 在
在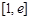 上是增函数,此时
上是增函数,此时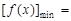
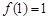 .
.
∴当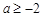 时,
时,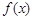 的最小值为1,相应的x值为1-------(7分)
的最小值为1,相应的x值为1-------(7分)
(3)不等式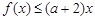 ,可化为
,可化为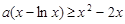 .
.
∵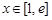 ,
∴
,
∴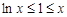 且等号不能同时取,所以
且等号不能同时取,所以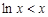 ,即
,即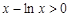 ,
,
因而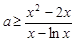 (
(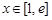 ),-----------------------(10分)
),-----------------------(10分)
令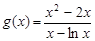 (
(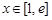 ),又
),又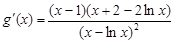 ,----12分
,----12分
当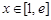 时,
时,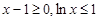 ,
,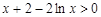 ,
,
从而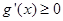 (仅当x=1时取等号),所以
(仅当x=1时取等号),所以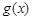 在
在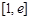 上为增函数,
上为增函数,
故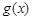 的最小值为
的最小值为 ,所以a的取值范围是
,所以a的取值范围是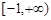 .(14分)
.(14分)


科目:高中数学 来源: 题型:
| 1 | 2x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| a(x-1) | x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2x-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com