
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD是矩形,平面PCD⊥平面ABCD,M为PC中点.求证: 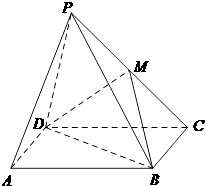
(1)PA∥平面MDB;
(2)PD⊥BC.
【答案】
(1)证明:连接AC,交BD与点O,连接OM,
∵M为PC的中点,O为AC的中点,
∴MO∥PA,
∵MO平面MDB,PA平面MDB,
∴PA∥平面MDB
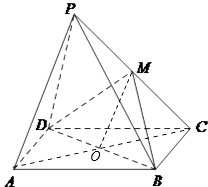
(2)证明:∵平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,BC平面ABCD,BC⊥CD,
∴BC⊥平面PCD,
∵PD平面PCD,
∴BC⊥PD
【解析】(1)连接AC,交BD与点O,连接OM,先证明出MO∥PA,进而根据线面平行的判定定理证明出PA∥平面MDB.(2)先证明出BC⊥平面PCD,进而根据线面垂直的性质证明出BC⊥PD.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


科目:高中数学 来源: 题型:
【题目】若函数f(x)=ax3+blog2(x+ ![]() )+2在(﹣∞,0)上有最小值﹣5,(a,b为常数),则函数f(x)在(0,+∞)上( )
)+2在(﹣∞,0)上有最小值﹣5,(a,b为常数),则函数f(x)在(0,+∞)上( )
A.有最大值5
B.有最小值5
C.有最大值3
D.有最大值9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面上的动点P(x,y)及两定点A(﹣2,0),B(2,0),直线PA,PB的斜率分别是 k1 , k2且 ![]() .
.
(1)求动点P的轨迹C的方程;
(2)设直线l:y=kx+m与曲线C交于不同的两点M,N. ①若OM⊥ON(O为坐标原点),证明点O到直线l的距离为定值,并求出这个定值
②若直线BM,BN的斜率都存在并满足 ![]() ,证明直线l过定点,并求出这个定点.
,证明直线l过定点,并求出这个定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 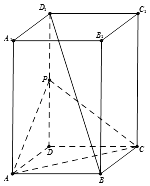
(1)求证:直线BD1∥平面PAC
(2)求证:平面PAC⊥平面BDD1B1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,当x∈[0,+∞)时,f(x)=2x+x﹣m(m为常数).
(1)求常数m的值.
(2)求f(x)的解析式.
(3)若对于任意x∈[﹣3,﹣2],都有f(k4x)+f(1﹣2x+1)>0成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在Rt△ABC中,AC=6,BC=3,∠ABC=90°,CD为∠ACB的平分线,点E在线段AC上,CE=4.如图2所示,将△BCD沿CD折起,使得平面BCD⊥平面ACD,连接AB,设点F是AB的中点. 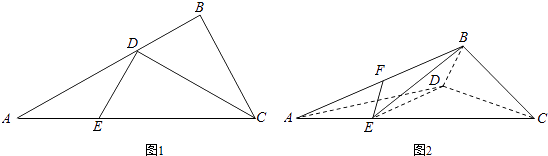
(1)求证:DE⊥平面BCD;
(2)若EF∥平面BDG,其中G为直线AC与平面BDG的交点,求三棱锥B﹣DEG的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com