
【题目】若函数f(x)=ax3+blog2(x+ ![]() )+2在(﹣∞,0)上有最小值﹣5,(a,b为常数),则函数f(x)在(0,+∞)上( )
)+2在(﹣∞,0)上有最小值﹣5,(a,b为常数),则函数f(x)在(0,+∞)上( )
A.有最大值5
B.有最小值5
C.有最大值3
D.有最大值9
【答案】D
【解析】解:令g(x)=ax3+blog2(x+ ![]() ),
),
其定义域为R,
又g(﹣x)=a(﹣x)3+blog2(﹣x+ ![]() )
)
=﹣[ax3+blog2(x+ ![]() )]=﹣g(x)
)]=﹣g(x)
所以g(x)是奇函数.
由根据题意: ![]() 在(﹣∞,0)上有最小值﹣5,
在(﹣∞,0)上有最小值﹣5,
所以函数g(x)在(﹣∞,0)上有最小值﹣7,
由函数g(x)在(0,+∞)上有最大值7,
所以f(x)=g(x)+2在(0,+∞)上有最大值9.
所以答案是:D.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知P是圆x2+y2=36的圆心,R是椭圆 ![]() 上的一动点,且满足
上的一动点,且满足 ![]() .
.
(1)求动点Q的轨迹方程
(2)若直线y=x+1与曲线Q相交于A、B两点,求弦AB的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长是2的正方体ABCD﹣A1B1C1D1中,E,F分别为AB,A1C的中点.应用空间向量方法求解下列问题. 
(1)求EF的长
(2)证明:EF∥平面AA1D1D;
(3)证明:EF⊥平面A1CD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某加工厂用某原料由车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品,每千克A产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天功能完成至多70多箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,甲、乙两车间每天获利最大的生产计划为( )
A.甲车间加工原料10箱,乙车间加工原料60箱
B.甲车间加工原料15箱,乙车间加工原料55箱
C.甲车间加工原料18箱,乙车间加工原料50箱
D.甲车间加工原料40箱,乙车间加工原料30箱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD是矩形,平面PCD⊥平面ABCD,M为PC中点.求证: 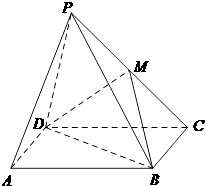
(1)PA∥平面MDB;
(2)PD⊥BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com