解:(1)∵f(x)=x
2+
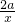
,
∴f′(x)=2x-
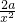
,
根据题意有f′(1)=2-2a=-14,解得a=8,
此时切点坐标是(1,17),故所求的切线方程是y-17=-14(x-1),即14x+y-31=0.
当a=8时,f′(x)=2x-
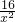
=
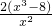
.
令f′(x)>0,解得x>2,令f′(x)<0,解得x<2且x≠0,
故函数f(x)的单调递增区间是(2,+∞);单调递减区间是(-∞,0)和(0,2).
(2)由(1)知f′(x)=2x-
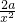
=
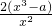
.
①若a≤1,则f′(x)>0在区间(1,2]上恒成立,f(x)在区间[1,2]上单调递增,函数f(x)在区间[1,2]上的最大值为f(2)=4+a;
②若1<a<8,则在区间(1,a)上,f′(x)<0,函数f(x)单调递减,在区间(a,2)上,f′(x)>0,函数f(x)单调递增,
故函数f(x)在区间[1,2]上的最大值为f(1),f(2)中的较大者,f(1)-f(2)=1+2a-4-a=a-3,
故当1<a≤3时,函数f(x)的最大值为f(2)=4+a,当3<a<8时,函数f(x)的最大值为f(1)=1+2a;
③当a≥8时,f′(x)<0在区间[1,2)上恒成立,函数f(x)在区间[1,2]上单调递减,函数f(x)的最大值为f(1)=1+2a.
综上可知,在区间[1,2]上,当a≤3时,f(x)
max=4+a;当a>3时,f(x)
max=1+2a.
不等式f(x)≤a
2-2a+4对任意的x∈[1,2]恒成立等价于在区间[1,2]上,f(x)
max≤a
2-2a+4,
故当a≤3时,4+a≤a
2-2a+4,即a
2-3a≥0,解得a≤0或a=3;
当a>3时,1+2a≤a
2-2a+4,即a
2-4a+3≥0,解得a>3.
故a的取值范围是(-∞,0]∪[3,+∞).
分析:(1)先求出其导函数,利用f′(1)=2-2a=-14,解得a=8,以及切点坐标和切线方程;再把a=8代入其导函数即可求出其单调区间;
(2)先求出其导函数,再利用分类讨论思想得到其在[1,2]上的单调性进而求出其最大值,最后再把问题转化为f(x)
max≤a
2-2a+4,即可求实数a的取值范围.
点评:本题主要考查利用导数求闭区间上函数的最值和利用导数研究函数的单调性以及利用导数研究曲线上某点切线方程,是对导数知识的综合考查,也是高考常考题型.

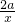 (a∈R).
(a∈R).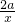 ,
,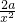 ,
,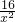 =
=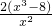 .
.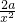 =
=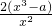 .
.

 高中必刷题系列答案
高中必刷题系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<