
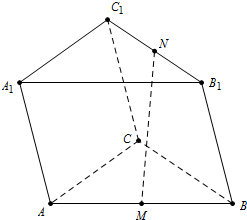
分析 (I)取A1C1的中点P,连接AP,NP.证得四边形AMNP为平行四边形.再由线面平行的判定定理即可得到;
(II)运用面面垂直的性质定理和线面垂直的性质和判定定理,即可得证.
(III)经N点向A1B1作垂线,设垂足为D,连接DM,可证ND∥CM,取A1B1的中点E,连接C1E,则ND∥C1E,由于N为C1B1的中点,E为A1B1的中点,利用三角形中位线定理即可得解$\frac{{B}_{1}D}{{A}_{1}{B}_{1}}$的值.
解答 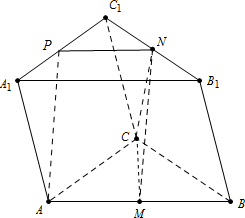 证明:(I)取A1C1的中点P,连接AP,NP.
证明:(I)取A1C1的中点P,连接AP,NP.
因为:C1N=NB1,C1P=PA1,
所以:NP∥A1B1,NP=$\frac{1}{2}$A1B1.
在三棱柱ABC-A1B1C1中,A1B1∥AB,A1B1=AB.
故:NP∥AB,且NP=$\frac{1}{2}$AB.
因为:M为AB的中点,所以AM=$\frac{1}{2}$AB.
所以:NP=AM,且NP∥AM.
所以:四边形AMNP为平行四边形.
所以:MN∥AP.
因为:AP?平面AA1C1C,MN?平面AA1C1C,
所以:MN∥平面AA1C1C.
(II)因为:CA=CB,M为AB的中点,所以:CM⊥AB.
因为:CC1=CB1,N为B1C1的中点,所以:CN⊥B1C1.
在三棱柱ABC-A1B1C1中,BC∥B1C1,所以:CN⊥BC.
因为:平面CC1B1B⊥平面ABC,平面CC1B1B∩平面ABC=BC.CN?平面CC1B1B,
所以:CN⊥平面ABC.
因为:AB?平面ABC,所以CN⊥AB.
因为:CM?平面CMN,CN?平面CMN,CM∩CN=C,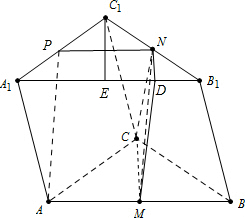
所以:AB⊥平面CMN.
(III)如图,经N点向A1B1作垂线,设垂足为D,连接DM,
因为:ND⊥A1B1,AB∥A1B1,
所以:ND∥CM,
取A1B1的中点E,连接C1E,则由C1E∥AB,
所以:ND∥C1E,
因为:N为C1B1的中点,E为A1B1的中点,
所以:$\frac{{B}_{1}D}{{B}_{1}E}=\frac{1}{2}$,$\frac{{B}_{1}E}{{A}_{1}{B}_{1}}=\frac{1}{2}$,
所以:$\frac{{B}_{1}D}{{A}_{1}{B}_{1}}$=$\frac{1}{4}$.
点评 本题考查线面平行的判定定理和线面、面面垂直的判定和性质定理,考查逻辑推理能力,注意定理的条件的全面性,属于中档题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | 1 | 2 | 3 | 4 | 5 |
| 政治分数x | 89 | 91 | 93 | 95 | 97 |
| 历史分数y | 87 | 89 | 89 | 92 | 93 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若p,则q”与命题“若非q,则非p”互为逆否命题 | |
| B. | 命题“?x∈R,x3-x2-1≤0”的否定是“?x∈R,x3-x2-1>0” | |
| C. | “若f′(x)=0,则x为y=f(x)的极值点”为真命题 | |
| D. | “am2<bm2”是“a<b”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com